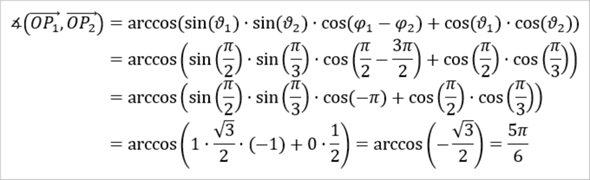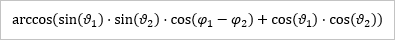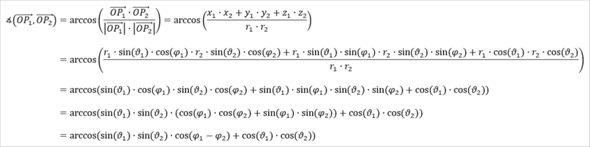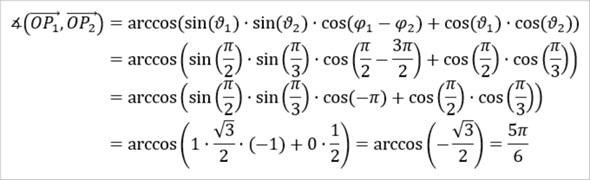Einfachste Methode, um den Winkel zwischen zwei Vektoren in Polarkoordinaten zu berechnen?
Hey,
Ich habe zwei Punkte:
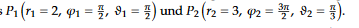
Und muss den Winkel zwischen r1 und r2 kennen. Ich weiß, dass das irgendwie durch das Umwandeln in kartesische Koordinaten funktionieren kann, aber ich überlege, ob das nicht auch anders geht, weil phi zB nur von -180 bis 180 gehen kann und ich ja auch Phi von beiden Punkten habe?
2 Antworten
Ich denke, dass man da (außer in speziellen Fällen) kaum darum herum kommt, zu kartesischen Koordinaten überzugehen und dann wie gewohnt das Skalarprodukt zu betrachten.
Man kann dies z.B. einmal in allgemeiner Form durchführen und die resultierenden Formeln dann für weitere Beispiele aufheben.
Für die Winkelberechnung kann man natürlich alle Vektorbeträge gleich 1 setzen und damit die Rechnungen auf die Winkel beschränken.
Nach meinem "Rezept" komme ich auf die Formel:
cos(alpha) = st1 st2 ( cp1 cp2 + sp1 sp2) + ct1 ct2
wobei st1 = sin(theta1), cp2 = cos(phi2) etc.
Benützte Konvention gemäß
Naja, wenn man das allgemein durchrechnet und vereinfacht, erhält man...
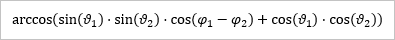
... für den Winkel zwischen den Ortsvektoren der beiden Punkte.
Möglicher Rechenweg:
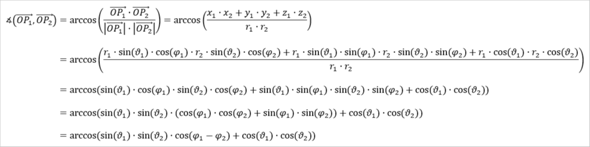
In Spezialfällen wie φ₁ = φ₂ könnte man das noch weiter vereinfachen. Allerdings ist dies bei der Aufgabe nicht der Fall, weshalb ich das so allgemein gelassen habe.
Im konkreten Fall erhält man damit dann jedenfalls...