Wie berechne ich am einfachsten die Winkel zwischen zwei Koordinatensystemen, um eine Transformationsmatrix aufzustellen?
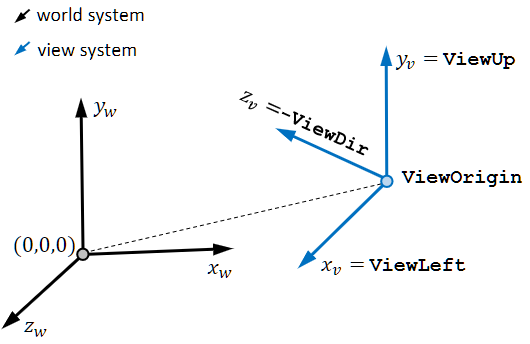
Ich habe zwei Koordinatensysteme, O (origin) und V (view). Sowohl der Punkt ViewOrigin, als auch die drei Vektoren, die die Achsen von V beschreiben, liegen in O-Koordinaten vor. Mein Ziel ist es, einen beliebigen Punkt p_v, der in V-Koordinaten vorliegt, nach O-Koordinaten zu transformieren. Dafür möchte eine homogene Transformationsmatrix aufstellen.
Das Ganze besteht ja im Grunde genommen aus einer Translation und drei Rotationen. Wenn ich die Winkel kenne habe ich kein Problem eine Rotationsmatrix aufzustellen, aber wenn ich nur die Achsen von V kenne, dann weiß ich nicht, wie ich auf drei passende Winkel komme, die O in V überführen (oder umgekehrt). Würde als Drehsystem z-y-z bevorzugen, aber andere Drehsysteme sind auch ok.
1 Antwort
Um die Winkel zwischen den beiden Koordinatensystemen zu ermitteln, müssen Sie die drei Vektoren bestimmen, die jeweils die Achsen beschreiben. Dazu müssen Sie die Richtung und Amplitude jedes Vektors berechnen. Nachdem Sie die drei Vektoren berechnet haben, können Sie den Winkel zwischen jedem Vektor bestimmen. Sie können dazu das Skalarprodukt, die Winkelfunktion oder den Satz des Kosinus verwenden. Wenn Sie die Winkel zwischen den Vektoren bestimmt haben, können Sie die Rotationen anwenden, um eine Transformationsmatrix aufzustellen. In der Regel verwenden Sie dazu das Drehsystem z-y'-z''. Dabei stehen die Winkel, die Sie zuvor berechnet haben, für die Eulerwinkel ein.