Drehmoment - wo ist der Winkel?
Ich hab diese Zeichnung in meinen Unterlagen gesehen und verstehe nicht ganz wie man auf die Formel M=Frsin(alpha) kommt..
Ist der Winkel immer zwischen F und r?
4 Antworten
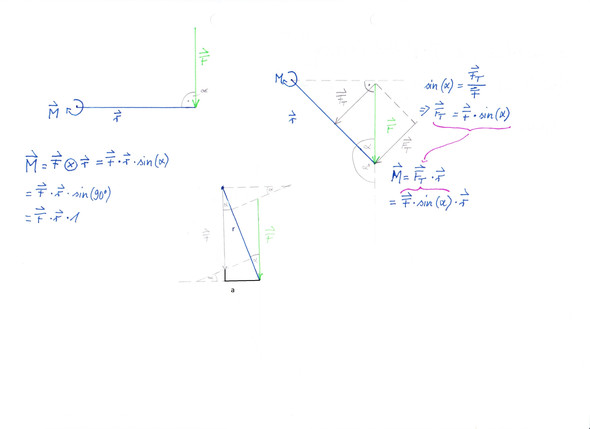
Ich hab dir mal zwei Skizzen gezeichnet.
Am besten stellst du dir ein Fahrradpedal dafür vor.
Bei der rechten Skizze müssen wir jetzt überlegen, welche Kraft ist denn überhaupt Drehmoment bildend ? -> Die Kraft die senkrecht (90°) zum Hebelarm steht. Deshalb müssen wir berechnen welcher Anteil der Kraft F senkrecht zu r steht.
Das ist sin(alpha) * F = F_T (T für tangential oder eben senkrecht Symbol)
Wie gesagt, ist es dem sinus egal, ob der Winkel oder der Gegenwinkel für die Rechnung benutzt wird.
In der Literatur oder auch bei Wikipedia findet man oft:
M = F * a
und dann a = sin(alpha) * r
Das habe ich dir in der Mitte versucht, etwas zu veranschaulichen.
Ich halte das aber für Quatsch. Es funktioniert mathematisch und theoretisch lässt sich aber schlecht auf die Realität übertragen.
Die Kraft F wird an den Mittelpunkt 0 angetragen und dann mit r * sin(@) ein neuer Hebelarm a berechnet.
Das erlaubt uns dann, die Kraft F zu drehen und an den Punkt 0a im rechten Winkel zu zeichnen wobei a auf r liegt.
Das ganze ist aus meiner Sicht viel unverständlicher und des Weiteren können in der Realität nicht mal so eben die Länge des Hebelarms und die Richtung der Kraft geändert werden.
Weshalb die Kräftezerlegung in F_T und F_r (hab ich nicht eingezeichnet liegt aber direkt auf r und trägt nicht zum Drehmoment bei) aus rechts viel nachvollziehbarer ist.
Ich hoffe, das ist jetzt etwas verständlich für dich :)
Bitte bitte :)
Nein, darfst du nicht.
Ist der Winkel zwischen F und F_T , müsste nach meiner Skizze der Tangens angewendet werden.
Das Drehmoment ist ein Kreuzprodukt, d.h., es werden die senkrecht aufeinander stehenden Komponenten multipliziert.
In der Skizze ist die typische Situation eines Kurbeltriebes gezeichnet. r und F stehen nicht senkrecht aufeinander.
Man könnte nun die Komponente von F ermitteln, die senkrecht auf r steht. Hier wird aber die senkrechte Komponente von r genommen. Beide Wege funktionieren.
Der "Innenwinkel" des r-Dreieckes beträgt 180 - α.
Die senkrechte Komponente von r(vektor) beträgt dann
r(vektor) * sin (180 - α)
Mit sin(180 - α) = sin α
ergibt sich dann aus:
M = F * r * sin(180 - α)
M = F * r * sinα
Danke! :) Damit wird aber der Abstand vom Drehpunkt vom Angriffspunkt berechnet?
Ach ok ich glaube ich verstehe jetzt die Skizze :D r ist die Länge des tatsächlichen Hebels, der Angriffspunkt wurde nach hinten verlängert und der Abstand von Angriffspunkt und Drehpunkt wird berechnet oder?
DANKE!
Genau das ist der Hintergrund...nächste Aufgabe bitte... ;-)
Wie würde man vorgehen wenn man die senkrechte Kraft berechnen will?
eine Senkrechte auf r zeigen. Winkel zwischen F und r ist alpha, der "gegenwinkel" ist 180 - alpha.
Wenn wir die Senkrechte eingezeichnet haben dann haben wir ein Dreieck mit F_s und F
cos(beta) = F_s/F
beta ist 90 -180 -alpha = -90 -alpha
Ist das minus falsch?
cos(-90 -alpha) = F_s/F
cos(-90 -alpha) = sin(alpha) ????
F_s = sin(alpha)*F
ISt das richtig überlegt? Die Frage die ich mir stelle ist halt, woher ich weiß welcher Winkel gemeint ist, es gibt ja zwei die zwischen r und F sind..?
Die Kraft könnte man zerlegen in eine parallel zu r(vektor), um damit die Lagerkräfte zu ermitteln und in eine Komponente senkrecht zu r(vektor). Mit der könnte man das Drehmoment ermitteln.
Die Kräftezerlegung läuft immer auf Trigonometrie hinaus.
Wenn man die Kraft F(vektor) zerlegt, ergibt sich für die parallele Kraft Fp:
Fp = F * sin(α-90) = F * cos α
Für die senkrecht zu r(vektor) stehenden Komponente Fs ergibt sich dann:
Fs = F * cos(α-90) = F * sin α
…logischerweise kommt auf dem Weg dasselbe Ergebnis für das Moment raus:
M = F * r = r(vektor) * Fs = r * F * sinα
Noch zur Frage welchen Winkel man meint.. Es gibt ja einmal den Winkel alpha zwischen r und F und den Winkel 180-alpha zwischen F und r. Woher weiß ich welcher gemeint ist?
Welchen Winkel man nimmt ist zunächst völlig egal. In der Praxis nimmt man den bequemsten. Letztlich hat man es bei der Vektorenzerlegung immer mit rechtwinkligen Dreiecken und den trigonometrischen Funktionen zu tun.
Da sin α = sin(180 - α) ist, ist es auch hier egal, mit welchem Winkel du rechnest. Es führen viele Wege nach Rom...
Ja. So ist M definiert.
.. das hätte ich jetzt nicht gedacht ..
das grüne soll r sein und das rote F, wie kommt man auf sinalpha
Die vektorielle Definition ist:
M = r x F
Du hast davon den Betrag hingeschrieben.
Der Sinus ergibt sich dann aus der Definition des Kreuzprodukts.
Wozu poste ich eine Skizze (zweimal), wenn man gar nicht darauf eingeht. Die Definition kenne ich wie gesagt doch! Es geht um die Skizze :/
Damit wird nur die tangentiale Kraftkomponente berechnet. Ohne das Bild erkennen zu können...
Ja danke, echt super Zeichnung.. Die Verwirrung lag noch anfangs, da ich mal eine Aufgabe berechnet habe wo der WInkel zwischen F_t und F eingezeichnet wurde. Da wusste ich nicht genau ob ich den sinus verwenden darf. Aber durch die Skizzen ist mir deutlich geworden, dass ich es nicht darf :D (oder?)