Bruchterme vereinfachen - Woher wissen wir, dass 1/5 = a/5a und 1/a = 5/5a?
Hallo! Ich habe gerade versucht, folgende Aufgabe zu lösen:

Ich wusste nicht, wie das gehen sollte, also habe ich mir die Lösung angesehen. Die korrekte Antwort wäre 1/5 gewesen. Aber bei der Erklärung der Lösung bin ich bereits beim ersten Schritt verwirrt:
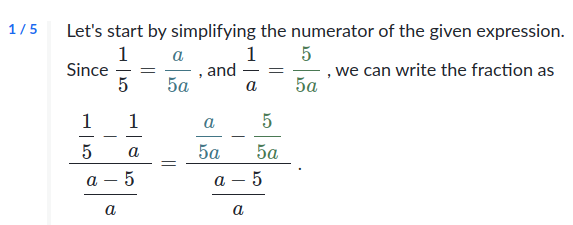
Wie komme ich darauf, dass 1/5 = a/5a und dass 1/a dasselbe ist wie 5/5a? Es steht da, als ob es selbstverständlich wäre, aber ich verstehe es nicht...

Die Schritte 2, 3 und 4 leuchten mir ein, ich kenne dieses Vorgehen bereits. Ich bin damit vertraut, zwei Brüche bei der Division in eine Multiplikation umzuwandeln.
Aber bei Schritt 5 bin ich erneut verwirrt. Warum ist a(a-5) = 1? Und 5a(a-5) = 5?
Nur zum Spaß habe ich etwas in 5a(a-5) als a eingegeben und das Ergebnis war definitiv nicht 5. Oder geht es gar nicht darum, dass man etwas in a eingeben sollen kann?
Generell finde ich es sehr schwierig, Bruchterme zu vereinfachen. Neben meiner bereits gestellten Frage könntet ihr mir eventuell ein paar Tipps geben, die euch geholfen haben, das Vereinfachen von Bruchtermen zu meistern?
Vielen Dank im Voraus!
5 Antworten
Die Tatsache, dass man Brüche erweitern und kürzen kann, ist eine Folge davon, wie die rationalen Zahlen definiert sind: zwei Brüche a/b und c/d mit a, b, c, d ganze Zahlen, b und d ungleich Null, werden als gleich angesehen, in mathematischer Terminologie: gehören derselben Äquivalenz-Klasse an, genau dann, wenn gilt: a*d = b*c. Man wählt in der Algebra eine scheinbar so komplizierte Definition, weil man dann auf dieselbe Art und Weise generell den Quotientenkörper eines beliebigen Integritätsringes bilden kann…
Wie komme ich darauf, dass 1/5 = a/5a und dass 1/a dasselbe ist wie 5/5a? Es steht da, als ob es selbstverständlich wäre, aber ich verstehe es nicht...
Da werden die Brüche erweitert. Nenner und Zähler werden mit dem gleichen Wert multipliziert.
In diesem Fall einmal mit a, und einmal mit 5
Aber bei Schritt 5 bin ich erneut verwirrt. Warum ist a(a-5) = 1? Und 5a(a-5) = 5?
Da wird gekürzt.
Nenner und Zähler werden durch a(a-5) geteilt.
Hallo,
im letzten Schritt kürzen sich (a-5) und a weg; es bleibt 1/5.
Herzliche Grüße,
Willy
simple the basics
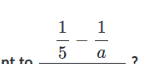
zwei Brüche zusammenfassen ? Hauptnenner finden . Der ist 5*a = 5a
Beide Brüche müssen erweitert werden . Der erste mit a , der zweite mit 5
Das ist ok , weil 1*a/5a ja weiter 1/5 ist
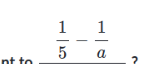
Woher wissen wir, dass 1/5 = a/5a und 1/a = 5/5a?
Das nennt sich "zwei Brüche auf gleichen Nenner bringen", um dann die Zähler addieren zu können und als einen einzigen Bruch mit dem gemeinsamen Nenner zu schreiben.