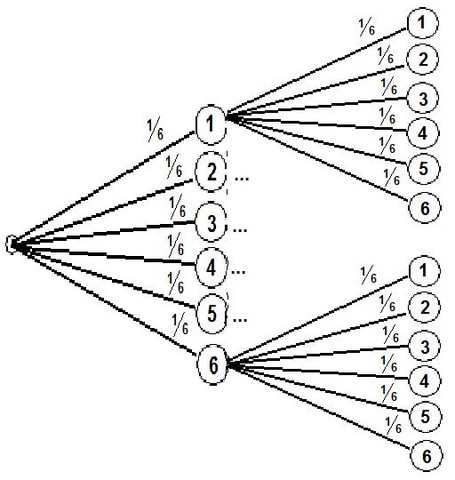
Baumdiagramm Wahrscheinlichkeit Mathematik 9. Klasse?
Hey Leute, ich brauche Eure Hilfe bei Aufgabe 2b. Könnte mir jemand erklären wie ich das Baumdiagramm zeichnen muss oder könnte mir die Lösung verraten? Danke schön im Voraus, LG
5 Antworten
Hallo,
zunächst gehen zwei Zweige ab:
Ereignis: Wurf einer 6 mit p=1/6
oder Ereignis: Wurf keiner 6 mit p=5/6
Wenn es nur darum geht, aufs Startfeld zu kommen, wäre der erste Zweig nach einer Stufe beendet, weil die ersehnte 6 ja gefallen ist und das Ziel erreicht wurde.
Vom anderen Ast gehen wieder zwei Äste ab, weil Du ja einen zweiten Versuch machen darfst.
Wieder hast Du 6 mit p=1/6 und keine 6 mit p=5/6
Wieder ist nach der 6 Schluß, während vom anderen Zweig wieder die gleichen zwei Zweige abgehen. Mit diesen beiden Zweigen endet dann der Baum, weil nach dem dritten Versuch entweder die 6 gefallen ist oder nicht.
Wenn sie fiel, ist die Figur aus dem Häuschen, wenn nicht, ist der Nächste an der Reihe.
Da Du nach einer 6 allerdings noch einmal würfeln kannst, kann das Spiel theoretisch auch länger dauern, bis alle Figuren draußen sind und Du irgendwann nicht mehr mit einer 6 weiterkommst, weil Du zu nah vor dem Ziel stehst.
Du kannst auch nach der jeweils ersten 6 noch einmal zwei Zweige anfügen.
Nach dem Ereignis: Keine 6 bricht der Baum dann aber sofort ab.
Herzliche Grüße,
Willy
Du hast zwei Zweige pro Spalte. Für jede Spalte gibt es die Möglichkeit 6: Der Spieler würfelt eine 6 und 6/: Der Spieler würfelt keine 6. Sobald er eine 6 würfelt, endet die Reihe, wenn er keine 6 würfelt gibt es wieder zwei Möglichkeiten: 6 und 6/. Der Spieler hat drei Versuche Zeit.
Die Wahrscheinlichkeit für eine 6 beträgt immer 1/6, für keine 6 beträgt sie 5/6.
An sich hast du immer zwei Äste, einen mit der Wahrscheinlichkeit 1/6 der zu 6 führt und einen mit der Wahrscheinlichkeit 5/6 der zum Gegenereignis führt.
Die Anzahl der Durchläufe ist allerdings abhängig von der Anzahl der Sechsen und kann deshalb nicht bestimmt werden. Deshalb kannst du auch kein Baumdiagramm zeichnen...
a) Erster Wurf: 5/6 chance keine 6, 1/6 Chance 6
Zweiter selbes
Dritter selbes
b)
Wurf 1
1/6 -> 6 Fertig
5/6 -> Keine 6 ->
Wurf 2
1/6 -> 6 Fertig
5/6 -> Keine 6 ->
Wurf 3
1/6 -> 6 Fertig
5/6 -> Keine 6 -> Zug vorbei
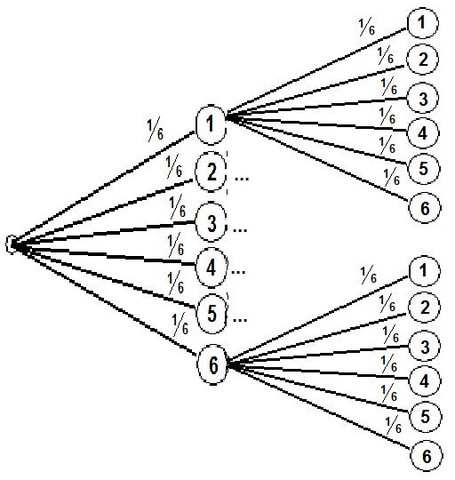
So ähnlich musst du das malen, wenn die 6 gefallen ist muss da natürlich kein Anschluss mehr ran.
