Ist das aufgrund der Fragestellung mit "momentane Zunahme" statt nur "Zunahme" und wie hätte die Fragestellung geheißen wenn der Wendepunkt gefragt ist?
Hey,
ich habe eine Frage zur folgenden Aufgabe a) auf dem Bild.
Gefragt ist die kleinste momentane Zunahme. In diesem Fall haben sie in der Lösung die 2.Ableitung gleich null gesetzt und mit der 3.Ableiting überprüft, ob es ein minimum ist. Die normale Vorgehensweise für Extrempunkte ist die erste Ableitung null zu setzen. An dieser stelle wird von f' ausgegangen,
Und wie hätte die Fragestellung geheißen wenn der Wendepunkt gefragt ist? Wäre das dann :Bestimmen sie die Produktionsmenge bei der die momentane Zunahme am geringsten zunimmt?

5 Antworten
f(x) sind die Kosten
die Ableitung davon, also f'(x) ist die (momentane) Kostenänderung
gesucht ist die Menge x, bei der die Kostenänderung am kleinsten ist. Es ist also das Minimum der Änderung, also der Extremwert von f'(x) gesucht.
Aus diesem Grund muss die Ableitung von f'(x). also f''(x) null gesetzt werden. Man berechnet also den Wendepunkt von f
mit der Formulierung "momentane Zunahme" hat das nichts zu tun, sondern damit, dass der Extremwert der Änderungsrate der gegebenen Funktion f gesucht ist. Die Änderungsrate ist aber schon die Ableitung f' und davon soll dann der Extremwert berechnet werden
Ich möchte gerne mal Käse und Rotwein verkosten. Wie Gott in Frankreich. Ob das was kostet? Wenn ja, wie viel?
Also der Text ist auch "falsch" in der Formulierung. Wasser ist ein natürliches Produkt. Das kommt halt einfach so vor. In der Mathematik ist ein Produkt das Ergebnis einer Multiplikation. Jedoch kann man Wasser oder andere Materialien nicht vervielfältigen. Es sei denn man ist Jesus oder kann zaubern. In der Herstellung von verpackten Artikeln mit Strichcode, die für den Konsum gedacht sind, geht es lediglich um die Zubereitung. Dazu verwendet man Zutaten. Zum beispiel Quellwasser, Brunnenwasser, oder von mir aus auch Abwasser aus der Chemiefabrik. Dann verarbeitet man die Mixtur in teilweise mehreren Schritten mittels der Verfahrenstechnik bis hin zum verkaufsfertigen Konsumprodukt. Verpackung drum. Strichcode drauf. Rauf auf die Palette. Rein in den Container. Rauf auf das Schiff. Und weiter in den Supermarkt oder Fachmarkt oder einfach bei Amazon bestellen.
Was ich (bzw mein Körper) wieder ausscheidet, von dem, was ich zuvor konsumiert (Lat.: Konsumare, Verschlingen) habe, landet hierzulande üblicherweise im Klo.
Ey, was ist denn "Sinn"? Also1: da gibt es den Zweck, das Ergebnis, das Produkt, die Zielführung, da wo man hin will oder was man haben will. Also2: Es gibt auch noch die Sinne der Sensorik: Sehen, hören, riechen, schmecken, fühlen. Und wer leckeren Braten sehen, riechen und schmecken will, der muss halt erstmal an den Braten rankommen.
So sieht der Graph aus:
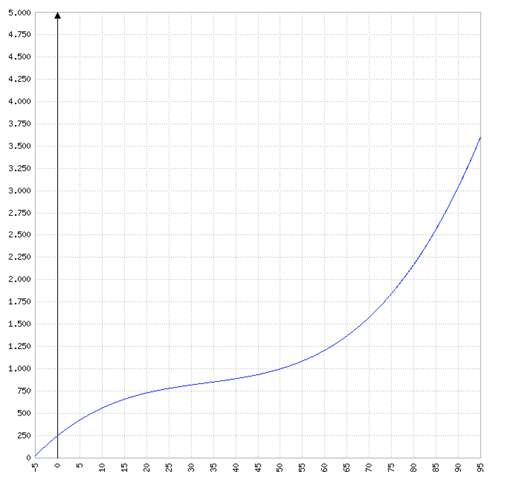
Der Graph stellt die absoluten Kosten (Gesamtkosten) der Produktion in Abgängigkeit von der Produktionsmenge dar.
f(0) = 250 sind die Kosten, die auch dann entstehen, wenn überhaupt nichts produziert wird. Diese 250.000 Euro sind daher die Fixkosten.
Die momentan Zunahme ist die momentane Änderungsrate und enstpricht der Steigung der Kurve. Die erhalten wir, indem wir f(x) einmal Ableiten:
Momentane Änderungsrate f'(x) = 0,03x^2 - 2x + 40
Von dieser Funktion sollen wir nun das Minimum ermitteln. Also leiten wir f'(x) ab uns setzen es zu 0. f'(x) einmal abgeleitet ergibt f' '(x):
f' '(x) = 0,06x - 2
0,06x - 2 = 0
0,06x = 2
x = 33,333
Ergebnis: die momentane Zunahme der Kosten ist bei einer Produktionsmenge von 33333 Hektolitern am geringsten.
Hinweis: Die Überprüfung, ob x = 33,333 ein Minimum oder ein Maximum darstellt, indem wir die zweite Ableitung der momentanen Änderungsrate bilden, also f' ' '(x), können wir uns in diesem Fall sparen, denn das sehen wir ja am Graphen, dass da die Kurve ihre flachste Stelle hat.
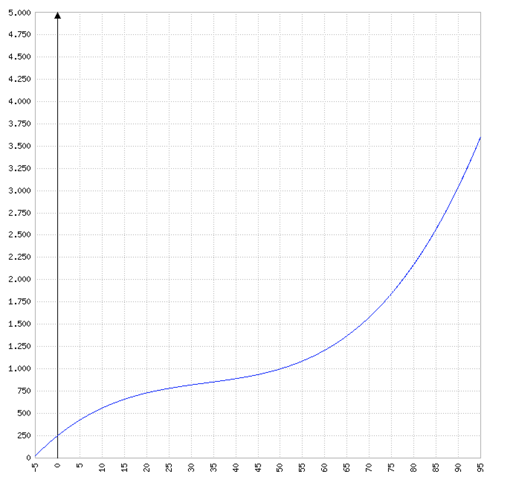
Danke, und wie wäre die Aufgabenstellung gewesen wenn ich den Wendepunkt berechnen muss
Das wäre derselbe Rechengang gewesen, bloß mit einer anderen Formulierung der Aufgabe. Der Wendepunkt der Kostenfunktion ist gleichzeitig das Minimum der momentanen Änderungsrate.
Wendepunkte sind immer auch gleichzeitig ein Extremum der Steigung der Kurve.
Lass dir das am Besten von deiner Mathelehrerin erklären.
"Die momentane Änderung" ist genau die erste Ableitung der Funktion. Demzufolge ist "die kleinste momentane Zunahme" ein Extremwert der Ableitung und folgerichtig wird auch die Ableitungsfunktion untersucht, nicht die Funktion selbst.
Es ist natürlich ungeheuer hilfreich für den Fragesteller wenn du denn Sinn der Frage anzweifelst. Bestimmt hat er in der Schule nächste Woche totalen Erfolg wenn er deine Weisheit im Mathematikunterricht wiederholt.
Ich bin nebenbei seit Jahrzehnten Gegner der übersteigerten Anwendungsorientierung im Mathematikunterricht, aber versuche dennoch zu helfen so gut es geht.