Stellen stärkster Zunahme/Abnahme?SOS?

Lösung:
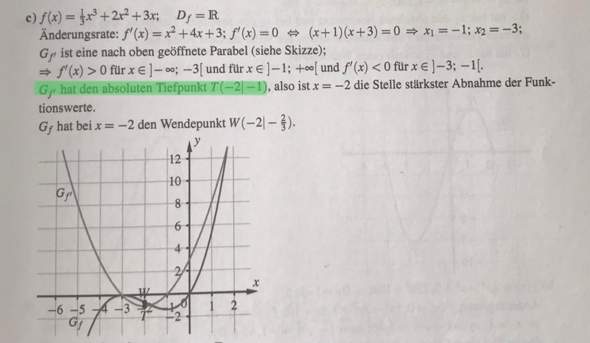
Es gilt ja folgendes:
• Wenn Gf‘ einen absoluten Hochpunkt besitzt, dann hat Gf eine Stelle stärkster Zunahme.
• Wenn Gf‘ einen absoluten Tiefpunkt besitzt, dann hat Gf eine Stelle stärkster Abnahme.
—> Wie kommt man bei c) darauf, dass es ein absoluter Tiefpunkt ist? Wieso berechnet man den?
—> Ich dachte, um die Stellen stärkster Abnahme/Zunahme zu berechnen, stellst Du die Wendepunkte fest und setzt die x-Werte derselben Stellen in die erste Ableitung ein. Diese ist für die Steigung zuständig. Wo du den höchsten Wert für die 1. Ableitung herausbekommst, ist die Stelle der stärksten Steigung.
DANKE!
2 Antworten
Extremstelle von f' ist das Minimum bei -2. Dort ist f'' = 0, und in diesem Bereich ist f' negativ.
Was du in dem zweiten --> schreibst ist richtig.
Bei c) wird der Tiefpunkt der Funktion f ermittelt, indem man die erste Ableitung f' = 0 setzt. Das ist auf alle Fälle ein Tief- oder Hochpunkt (Sattepunkte ignoriere ich jetzt einfach mal). Ist gleichzeitig die 2te Ableitung f'' > 0 , dann ist es ein Tiefpunkt (Linkskurve). Ist f'' < 0, dann ist esxein Hochpunkt ( Rechtskurve).
Steht alles in meinem Text. Ich hoffe doch, dass du weißt was die erste, die zweite Ableitung ausdrückt.
Überlege doch mal. Eine Funktionskurve kann öfters mal die Richtung ändern. Mal hoch mal runter. Es ist nicht gesagt, daß die Kurve an den Rändern ( des Def.bereichs) die höchsten oder niedrigsten Werte annehmen muß.
Bei c) ist die Definitionsmenge nicht eingeschränkt, also Df = R, dann kann man ja nicht vergleichen, wo der höchste/niedrigste Wert für die 1. Ableitung ist, da man ja keine Randwerte zum Vergleichen hat. Wie soll man dann wissen, ob eine Stelle stärkster Zunahme/Abnahme vorliegt.
Können Sie mir bitte das beantworten?