Additionsverfahren Aufgabe rechnen?
Hallo liebe Mathegenies, :D
Ich habe eine Frage zu dieser Aufgabe.
Das Bild das unten zu sehen ist ist die Aufgabenstellung, die vorgegebene ist. Wir sollen diese Aufgabe nun mit dem Additionsverfahren rechnen. Jedoch hab ich schon zich verschiedene Wege probiert und komm nie auf das richtig Ergebnis (Ergebnisse sind bei den Aufgaben vorgegeben zum abgleichen). Könnte mir wer den richtigen Ansatz oder vll. die ganze Aufgabe hinschreiben damit ich diese versteh und die nächste alleine machen kann. Vielen Dank.
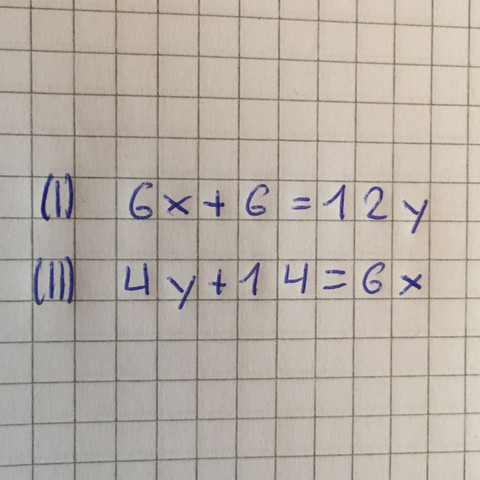
5 Antworten
1. Schritt: Das "lineare Gleichungssystem",LGS, aufschreiben,wie es im Mathe-Formelbuch steht
hier ist ein LGS mit 2 Unbekannte,x u. y und 2 Gleichungen.Das steht im Mathe-Formelbuch wie folgt:
1. a11*x+a12*y=b1
2. a21*x+a22*y=b2
nun mit deinen Beispiel ergibt
1. 6*x-12*y=-6
2. -6*x+4*y=-14 beide Gleichungen addiert ergibt
3. 0-8*y=-20 also y=-20/-8=2,5
hier sehen wir schon,daß 6*x+(-6*x)=0 ergibt. Wir brachen also Gleichung 1. nicht mit einen passenden Faktor multiplizieren.
HINWEIS: Im Normalfall muss man Gleichung 1. mit einen Faktor multiplizieren , nennen wir ihn "c". Hier muß c so gewählt werden ,daß
(a11*x)*c+a21*x=0 wird, also c=-a21/a11 wobei a11 ungleich Null sein muß!
Das erreicht man,indem man einfach die Reihenfolge der Gleichungen vertauscht!
also,bei dir brauchen wir nicht "c" ermitteln.
nun die beiden Gleichungen addieren
6*x+(-6*x)=0 und -12*y+4*y=-8*y und -6+(-14)=-20
dies ergibt Gleichung 3. 0-8*y=-20
ergibt y=-20/(-8)=2,5
in 1. ergibt 6*x-12*2,5=-6 ergibt x=(-6+12*2,5)/6=4
also x=4 und y=2,5
Mach die Probe und prüfe auf Rechen-u.Tippfehler.
TIPP:Besorge dir auf jeden Fall privat ein Mathe-Formelbuch aus einen Buchladen,kosten so 30 Euro.
Da brauchst du nur abschreiben.Alle Formeln,die du brauchst,stehen da drin.
Dafür bekommst du dann so 600 Seiten mit Formeln,Zeichnungen und kleinen beispielaufgaben.
Du mußt dann dieses Buch durcharbeiten,damit du weißt,wo welche Formeln stehen.
Das Buch ist in Kapitel unterteilt,"Geometrie","Algebra","Funktionen","Differentialrechnung""Integralrechnung"
sehr wichtig die "Differentationsregeln","elementare Ableitungen" und "Integrationsregeln","Anwendung Integralrechnung"
Zunächst stellst du (II) ein wenig um
(II) 4y + 14 = 6 x -> 6x -14 = 4y
nun rechnest du (I) - (II) (umgestellte Version)
6x + 6 = 12 y
-(6x-14) = -4y
20 = 8 y
5/2 = y
Einsetzen in (I)
6x + 6 = 12 y = 12 * 5 / 2 = 30 | -6
6x = 24
x = 4
Probe durch Einsetzen von x und y in (II)
http://dieter-online.de.tl/2-Gleichungen-mit-2-Unbekannten.htm
Hier könnte man sogar sehr schnell mit dem Gleichsetzungsverfahren arbeiten (6x), aber es soll ja das Additionsverfahren sein.
Für das Additionsverfahren gibt es einen strengen Aufbau. Alle Unbekannten stehen auf der linken Seite untereinander:
I 6x - 12y = -6
II -6x + 4y = -14
Gewöhnlich muss man die Gleichungen noch multiplizieren, um identische Terme bekommen. Hier kann man sofort addieren.
I+II -8y = - 20 | /(-8)
y = 2,5 oder = 5/2 , falls man Brüche bevorzugt
Einsetzen in I: 12 * 2,5 = 30
6x - 30 = -6 | +30
6x = 24
x = 4
Vielen Herzlichen dank 😊
Meiner Meinung nach die beste Erklärung 👍🏼
Könnten Sie mir dennoch erklären wie sie die Aufgabe einfacher mit dem Gleichsetzungsverfahren rechnen wollten?
Das "Sie" lassen wir mal weg. Ich bin hier Volens oder Dieter.
Gleichsetzungsverfahren:
I 6x = 12y - 6
II 6x = 4y + 14
Da 6x = 6x, sind auch die rechten Seiten einander gleich:
12y - 6 = 4y + 14 | -4y | +6
8y = 20 | /8
y = 2,5
Dann x errechnen wie oben.
---
Und auch das Einsetzungsverfahren wäre hier leicht möglich, da ein Term für 6x vorliegt.
(Gleichsetzung bzw. Einsetzung heißt ja nicht, dass man eine Unbekannte auf x oder y herunterrechnen muss. Man kann auch Vielfache oder andere zweckmäßige Umformungen verwenden, wenn sie gleich sind.)
Ich gebe dir mal einen Ansatz. Du musst versuchen durch das Additionsverfahren eine der beiden Variablen zu elliminieren. Demnach wäre es ja ganz praktisch, wenn das x wegfallen würde. Also stellt man erst mal beide Gleichungen so um, dass alles auf der linken Seite steht und auf der rechten Seite nur noch ... = 0.
Dann fällt dir vielleicht auf, dass bei Addition beider Gleichungen das x direkt herausfällt, und man dann y berechnen kann.
Subtrahiere von der ersten Gleichung 12 y und 6 x
Teile diese Gleichung durch 3
Addiere dann die beiden Gleichungen
Dann hast Du eine Gleichung mit einer Unbekannten! Bin übrigens kein Mathegenie.
Wir haben kein Formelbuch, bei uns in der Schule (Realschule) bekommt man das erst in der 3. Schulaufgabe in der 9. Klasse. Wir schreiben am Montag die 1. Aber viele Vielen dank, ich meine verstanden zu haben.