Addition von zwei komplexen Zahlen in Exponentialform (unterschiedliche Beträge, unterschiedliche Winkel) - wie vorgehen?
Hallo liebe Mathematiker,
ich bin im Internet auf die folgende Rechnung zu oben genanntem Thema gestoßen:
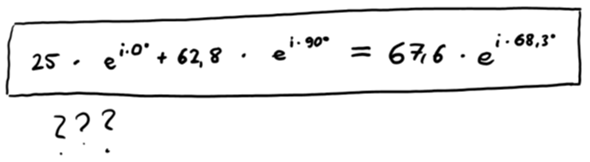
Meine Mathematik-Vorlesungen im Studium sind leider schon etwas länger her, aber soweit ich mich entsinnen kann, konnte man eine Addition bzw. Subtraktion von komplexen Zahlen nur vereinfachen, wenn entweder deren Beträge oder deren Winkel gleich sind. Bei diesem Beispiel ist beides nicht der Fall und trotzdem scheint eine Vereinfachung möglich zu sein.
Kann mir jemand kurz auf die Sprünge helfen und erklären, welche Regel hier zu Grunde liegt?
Besten Dank im Voraus.
Mit freundlichen Grüßen,
carbonpilot01
2 Antworten
Hallo,
siehe Antwort von tunik.
Darüberhinaus:
Hier liegt ein besonderer Fall vor. Du hast zwar nicht die gleichen Exponenten von e, aber Du hast als Winkel einmal 0° und einmal 90°.
Nun ist e^(i*phi) das Gleiche wie cos (phi)+i*sin (phi). Andererseits setzt sich eine komplexe Zahl aus einem Real- und einem Imaginärteil zusammen.
Der erste Summand ist 25*e^(i*0°). Das ergibt 25*(cos (0°)+i*sin (0°)).
Da cos (0°)=1 und sin (0°)=0, fällt hier der Imaginärteil weg, so daß 25*1 als Realteil übrigbleibt.
Beim zweiten Summanden ist e^(i*90°)=cos (90°)+i*sin (90°)=0+i*1, also i.
Hier hast Du nur einen Imaginärteil, der noch mit 62,8 multipliziert wird.
Die komplexe Zahl 25+62,8i aber ergibt in Polarkoordinaten den Betrag dieser Zahl
mal e^(i*arctan (62,8/25))=Wurzel (25²+62,8²)*e^(i*68,3°).
Du kannst in diesem speziellen Fall also sofort Wurzel (25²+62,8²)*e^(i*arctan (62,8/25)°) rechnen ohne den Umweg über die kartesische Darstellung.
Herzliche Grüße,
Willy
Das kann er blöderweise nicht, obwohl er eine Funktion für komplexe Zahlen hat. Er kann auch keine komplexen Wurzeln ziehen.
Eigentlich ein Superrechner - aber diese Funktionen vermisse ich an ihm.
Das ist schade. Das heißt, es gibt bei derartigen Additionen von komplexen Zahlen in der Exponentialform eigentlich keine Möglichkeit, wie ich mir mit der Komplexe-Zahlen-Funktion meines Taschenrechners Arbeit ersparen kann?
Ich muss tatsächlich zuerst über die Polarform in die kartesische Form umwandeln, dann in der kartesischen Form die Addition durchführen und schließlich mittels Betrag- und Winkelberechnung wieder in die Exponentialform umwandeln?
Sieht so aus, ja. Die App TechCalc+, die ich auf meinen Kindle-Fire geladen habe für ein paar Euro, kann das.
Hallo Willy1729, ich habe nun herausgefunden, dass der CASIO fx-991DEX CLASSWIZ doch komplexe Zahlen in Exponentialform addieren und subtrahieren kann! Falls Du wissen möchtest, wie das geht, schreibe mir mal.
Man muss hier über die kartesische Form gehen.
Die Umwandlung aus der Exponentialform und die Addition ist hier trivial:
25 + 62,8 * i
Das wandelt man zurück in r = e^(i*w) mit
r² = 25² + 62,8²
tan(w) = 62,8 / 25
Hallo Willy1729,
super Erklärung, vielen Dank. Weißt Du zufälllig, ob diese Rechnung auch direkt mit meinem Taschenrechner (CASIO fx-991DEX CLASSWIZ) möglich gewesen wäre oder kann ich diesen nur mit der kartesischen Form "füttern"? ;-)
Beste Grüße,
cabonpilot01