Ableitung an einer Stelle mit Differenzenquotient?

Wie kann man die Funktionen f(x)=√(5-x) an x0=1

h(x)=4/(4+x) an x0=4

und g(x)=1/x^2 an x0=-2

mithilfe des Differenzenquotienten ableiten?

Die Ableitungsfunktion auszurechnen und Werte einzusetzen macht mir kein Problem . Allerdings habe ich Schwierigkeiten beim Umformen, wenn man die Aufgaben mithilfe des Differenzenquotienten lösen soll.

Answer 1

[mihisu]

Bei Grenzwerten mit Wurzeldifferenzen ist es häufig hilfreich entsprechend der dritten binomischen Formel zu erweitern. Im Folgenden habe ich erst einmal recht allgemein mit x_0 gerechnet und erst am Ende x_0 = 1 eingesetzt. Man hätte aber auch schon vorher x_0 = 1 einsetzen können.

============

Brüche kann man subtrahieren, indem man sie auf einen gemeinsamen Nenner erweitert und dann die Zähler subtrahiert.

============

Auch beim letzten Differentialquotienten hilft wieder das erweitern auf einen gemeinsamen Nenner, die dritte binomische Formel und schließlich ein kürzen mit (x - x_0).

Comments

[Bienenstock56]

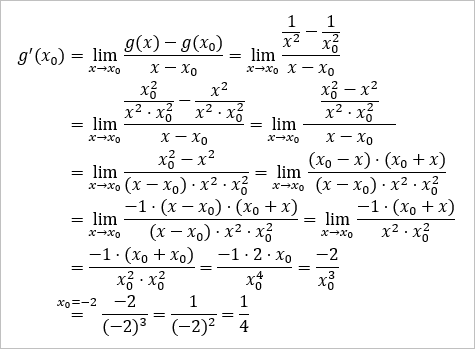
Herzlichsten Dank! Hab es nun komplett verstanden.

Answer 2

[precursor]

Falls das darauf hinaus läuft, dass ihr die Kettenregel mithilfe der h-Methode beweisen sollt, dann schau mal hier :

http://micbaum.y0w.de/uploads/DHBWStuttgart-Extra02-h-Methode.pdf

Sollte ihr einfach nur den Differenzenquotienten ausrechnen, dann geht das folgendermaßen :

Ich verwende den zentralen Differenzenquotienten :

m = (f(x_0 + h) - f(x_0 - h)) / (2 * h)

Ich zeige es dir an der Funktion f(x)=√(5 - x)

x_0 = 1

h = 0.1

m = (√(5 - (1 + 0.1)) - √(5 - (1 - 0.1))) / (2 * 0.1) ≈ - 0,25001953659254395790

h = 0.01

m = (√(5 - (1 + 0.01)) - √(5 - (1 - 0.01))) / (2 * 0.01) ≈ - 0.25000019531303405958

h = 0.001

m = (√(5 - (1 + 0.001)) - √(5 - (1 - 0.001))) / (2 * 0.001) ≈ -0,25000000195312505341

Man lässt h also systematisch kleiner werden.

Ich denke ab hier brauche ich nicht mehr weiter machen, Man sieht, dass das gegen

- 0,25 = - 1 / 4 strebt.

Und das ist der Funktionswert der ersten Ableitung f´(x) an der Stelle x = 1

Man sollte vorsichtig sein, verwendet man einen Rechner mit ungenügender Rechengenauigkeit, dann kann es zu Stellenauslöschungen kommen.

Answer 3

[poseidon42]

a)

(f(x0+h) - f(x0))/h = (sqrt(4 - h) - sqrt(4))/h = (sqrt(4 - h) - 2)/h

= [(sqrt(4 - h) - 2)*(sqrt(4 - h) + 2)] / [h*(sqrt(4 - h) + 2)]

= [4 - h - 4] / [h*(sqrt(4 - h) + 2)] = (-1)/(sqrt(4 - h) + 2) ---> (-1)/(sqrt(4) + 2) = (-1)/4

für h --> 0. Damit folgt also:

f´(1) = (-1)/4

b)

(g(x0+h) - g(x0))/h = (1/(-2 + h)^2 - 1/4)/h = [4 - (-2 + h)^2] / [4*h*(-2 + h)^2]

= [4 - (4 - 4h + h^2)] / [4*h*(-2 + h)^2] = [4h - h^2] / [4*h*(-2 + h)^2]

= 1/[(-2 + h)^2] - h / [4*(-2 + h)^2] ---> 1/(-2)^2 = 1/4 für h --> 0.

Damit gilt also:

g´(-2) = 1/4

c)

(h(x0+h) - h(x0))/h = (4/(8 + h) - 1/2)/h = [8 - (8 + h)] / [2*h*(8 + h)]

= (-h)/[2*h*(8 + h)] = (-1)/[2*(8 + h)] ---> (-1)/(2*8) = (-1)/16 für h --> 0.

Damit gilt also:

h´(4) = (-1)/16

Answer 4

[Applwind]

Wie lautet der Differenzenquotient?

Weißt du wie du einen Quotienten rationalisierst ?

Weißt du wie du einen Hauptnenner bildest?

Beachte : x2-x1=:h

Woher ich das weiß: Hobby – Schüler.