Wenn du in IR bist und du etwas wie x^2 = -36 hast, dann ist die Rechnung vorbei, weil für jedes x aus IR gilt (-x)^2 = x^2.
Bist du in C, dann gilt :
sqrt(-36) = sqrt(36*e^(pi*i)) = 6 * e^(pi*i/2) = 6i
r = lim n -> inf (2^(n-1)/(2n-1))/(2^n)/(2n+1))
= lim n -> inf (2^(n-1) * 2n)/((2n-1)*2^n)
= lim n -> inf (1/2*(2n+1))/(2n-1)
= lim n ->inf ((2n+1)/(2*(2n-1))
= lim n -> inf (n(2+1/n)/(n(4-2/n))
= 1/2
=> r = 2
Selber prüfen! (z.b mit Cauchy Hadamard)
Konvergenz gibt es dann bei allen x mit |x-3| < 2
Ich nutze immer mathematische Definitionen und modifiziere sie leicht, vor allem weil manche Websites, damit nicht klarkommen.
Wenn einer „dumm“ ist, dann ist es dein Lehrer. Intelligenz ist nämlich nicht gleich Intelligenz, denn sie „spaltet“ sich in verschiedene Sektoren, die wiederum unterschiedlich ausgeprägt sind.
Deinem Lehrer unterstelle ich mal dreist, dass er keine „zwischenmenschliche“ Intelligenz hat.
Ich empfehle dir, dass du deine Stärken ausspielst, denn jeder hat welche und etwas verstehen kann auch durch psychische bzw. emotionale Komponenten beeinflusst werden.
+ tan^(-1) (…….)
*5
/0,9^2
f(x) = 3x^4 + 2x^3 + 0 * x^2 + 5x^1 + 7*x^0
Ich kann mich noch gut an meine Analysis I Klausur erinnern. Davor viel relativ viel gelernt und Ende trotzdem dumme Fehler gemacht…. Tja, wenn die Sinusfunktion plötzlich mit der Potenzregel für Potenzen differenziert wird….
In der Regel hast du gute Karten, wenn du die Übungsaufgaben gut lösen könntest.
Es geht hier nicht mehr um schulische Sachen, wenn du schon solche Aussagen tätigst. Ich empfehle dir dringend einen entsprechenden Psychologen bzw. Psychiater aufzusuchen. Es gibt immer Wege deine Ziele zu erreichen.
Hier der Nachweis, wahrscheinlich nicht verständlich, aber es stimmt. Die Funktion f(x) = cos(x) ist eine gerade Funktion und + 1, wegen 1*x^0 und 0 € 2IN auch.
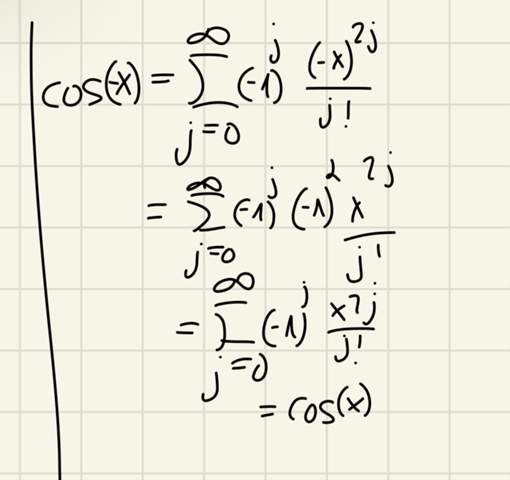
Vorgehen ist hier immer gleich. Ermittle den Schnittpunkt mit der Y-Achse, das ist dann dein „a“, weil f(0) = a.
Um „b“ ermitteln zu können, nimmst du dir einen beliebigen, gut ablesbaren Punkt vom jeweiligen Graphen und setzt es in die Gleichung ein und löst sie nach „a“ auf.
bsp:
a) f(0) = 2 und P(2/8)
8 = 2 * b^2
4 = b^2
2=b (-2 nicht zulässig)
f(x) = 2 * 2^x
usw
enn Stückvektor der Geraden in der Ebene liegt, also
E: 3x1+x2-4x3= 1 wäre
3 + 2 -4a = 1 <=> a = 1
und wenn Skalarprodukt aus NV und RV null ergibt :
( 3 1 -4) • (2 t 1) = 0
=> 6 + t - 4 = 0
=> t = -2
Also : g : x = ( 1 2 1) + r * ( 2 -2 1) liegt in E.
Folgt aus den Potenzgesetzen :
a^m * b^m = (a*b)^m
Nehmen wir a,b>=0 , m € Q
a^(1/2) * b^(1/2) = (a * b)^(1/2)
und a^(1/2) = sqrt(a)
und weil sqrt(10) nicht von y abhängig, gilt Faktorregel.
A(2/20) ; B(4/80)
80 = a * b^4
20 = a * b^2
=> 4 = b^2 => b = 2 (-2 unzulässig)
20 = a * 4
5=a
f(t) = 5*2^t
f(0) und f(11/2) auswerten
Wende auf beiden Seiten „arcsin(…)“ bzw „arccos(…)“ bzw. häufig aber falsch und irreführend „sin^(-1)“ bzw. „cos^(-1)“ auf die jeweilige Gleichung an.
Für den Sinus gilt : Weitere Lösungen erhält man durch die Addition von Vielfachen der Periode, hier „2pi“. Die „zweite“ Lösung indem man von pi die obere Lösung abzieht.
Für den Kosinus : Gleiches wie oben, nur die zweite Lösung wird mit einem „Minus“ versehen, entsprechend mit der Addition der Periode.
bsp : sin(a) = 0,2588 <=> a = arcsin(0,2588) oder 15° und Pi - arcsin(0,2588) also 165°.
Verwende einfach ∫ y‘(x)/(y(x)) dx = ln(|y(x)|) + C
Das mit dem rechnen von Differentialen bereitet mir richtige Bauchschmerzen.
Machen wir es kurz :
Ist f(x) = an * x^n + an-1 * x^(n-1) + …. + a1*x + a0 mit aj € IR von j = 1 ,….. , n und n € IN mit an ≠ 0 dann heißt f ganzrational.
Deine Exponenten sollen also natürliche Zahlen sein und in dieser Form gebracht werden.
Für a ∈ ℝ gilt sqrt(a^2)= |a| also ist |a| = sqrt(112). Nehmen wir wie oben a > 0 an, dann ergibt sich a1= sqrt(112)
Edit : Folgenkriterium ist gar nicht notwendig, weil du es einfacher mit ℇ-δ Kriterium lösen kannst. Für (x,y)≠ (0,0) nutzt du die Stetigkeitssätze in IR und für (x,y) = (0,0) beachtest du zuerst, dass (x+y)^2 ≥ 0 für alle x,y < 0 und (x-y)^2 ≥ 0 für alle x ,y ≥ 0. Dann erhältst du eine Abschätzung, damit du dein δ finden kannst.
Gar nicht, weil die Operation so nicht definiert ist. Vielleicht meintest du aber das Skalarprodukt zweier Vektoren??
“Die Summe der Quadrate zweier aufeinanderfolgender ganzer Zahlen x und x + 1“
x^2 + (x+1)^2
„ist um 10 größer als die größere der beiden Zahlen“
Die Summe ist also um zehn größer als x + 1 , dann muss damit die Gleichung
x^2 + (x+1)^2 + ? = x + 1 ? = -10 sein, weil dann ist x + 1 nicht um 10 größer als die linke Seite und alles stimmt
x^2 + (x+1)^2 - 10 = x + 1
<=>
x^2 + x^2 + 2x -9 = x + 1
<=>
2x^2 + x -10 = 0
x1/2 = -1 + /- sqrt(1-4*2*(-10)) * 1/4
x1 = (-1 + 9) /(4) = 2
x2 = (-1-9)/(4) < 0
Die gesuchte Zahl ist zwei.
Probe :
2^2 + 3^2 = 13
und 13 ist um 10 größer als 3