Woher kommt die Formel für e als funktionaler Grenzwert?
Hi,
ich wollte fragen, wie man die Formel für e als funktionalen Grenzwert herleiten kann.
Also e wird ja definitert als https://wikimedia.org/api/rest_v1/media/math/render/svg/c16ee0bbc785080c215034407389c3551064a4dc
Aber ich frage mich wie man von dieser Darstellug auf e = lim t->unendlich (1+1/t)^t kommt?
Liebe Grüße
2 Antworten
Eulerzahl e¹=e=2,71828.. (1+1/n)^(n) mit n → unendlich
Trick e²=7,387.. e^(ln(7,387)=e²
e^(ln[(1+1/n)^n] Logarithmengesetz log(a^(x))=x*log(a)
n*ln(1+1/n)
Trick n/1=1/(1/n)
1/n*ln(1+1/n)=lim ln(1+1/n)/(1/n) mit n → unendlich
ln(1+0)/0=ln(1)/0=0/0 ein Fall für l´Hospital lim f(x)/g(x)=f´(x)/g´(x)
g(n)=1/n abgeleitet nach der speziellen Quotientenregel (1/v)´=-1*v´/v²
g´(n)=-1/n²
f(n)=ln(1+1/n) nach der Kettenregel f´(x)=z´*f´(z)
Substitution (ersetzen) z=1+1/n → z´=dz/dn=-1/n²
f(z)=ln(z) → f´(z)=1/z siehe Mathe-Formelbuch,elementare Ableitungen
f(x)=ln(x) → f´(x)=1/x
f´(n)=-1/n²*1/(1+1/n)
lim f´(n)/g´(n)=[-1/n²*1/(1+1/n)]/(-1/n²)=(-1)/(-1)*n²/n²*1/(1+1/n)=1/(1+1/n)
n → unendlich
1/(1+0)=1/1
also e^(ln(1+1/n)^(n)) mit n → unendlich ergibt e¹=e=2,71828..
https://de.wikibooks.org/wiki/Mathe_f%C3%BCr_Nicht-Freaks:_e-Reihe
zeigt schon mal ,dass es nicht so einfach ist.
e als zahl kommt rechnerisch wohl aus
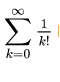
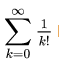
Man kann ja auch bei der Formel (1+1/n)^(n) eine Wertetabelle aufstellen und dann sieht man,dass sich bei n>1000 nich mehr viel ändert,als wenn man komplizierte Formeln rechnet,die man nich versteht
Das kann man auch bei Grenzwerten machen,wo z. Bsp. x → unendlich geht.
Also,große Werte für x einsetzen
Schreib bei mir ab und notiere in deinen Unterlagen,dann informiere die anderen Schüler.