Wie zeichnet man eine Tangente ein um die Steigung zu bestimmen?
Also gegeben ist ein Schaubild, eines Graphen. (Das Schaubild seht ihr in meiner vorletzten Frage, falls das für die Beantwortung dieser Frage wichtig ist)
gesucht ist die Steigung bei f‘(1).
jetzt muss ich die tangente einzeichnen um somit die Steigung ablesen zu können (wie man die steigung mithilfe einer tangente abliest weis ich) leider bin ich mir grad nicht Safe, wie man diese tangente einzeichnet.
also sie muss die Funktion bei Punkt 1 berühren, weil ja die Steigung bei f‘(1) gesucht ist, aber da muss es ja noch irgendeinen anderen Punkt geben wo sie durch muss, weil ja sonst könnte ich die ja fast zeichnen wie ich will 😅
ja wäre cool Wenn mir das kurz jemand erklären könnte
2 Antworten
Das kann man (es geht sicher um die Exponentialfunktion) nur mit "Augenmaß" zeichnen; so, dass in diesem Fall die Tangente auch die anderen Punkten drumherum nicht schneidet... Auf die rechnerische Steigung von 1,39 wirst Du zeichnerisch nur näherungsweise kommen.
aber da muss es ja noch irgendeinen anderen Punkt geben wo sie durch muss,
den hast du aber nicht , drum kannst du , ganz matheuntypisch , nur nach Gefühl gehen.
mihisu hat doch schon alles gezeigt.
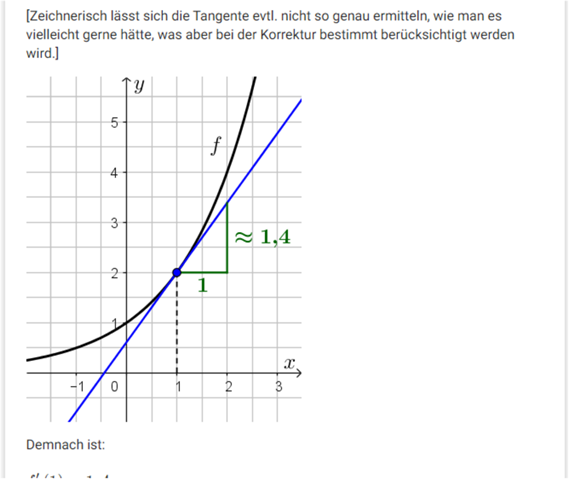
mehr geht nicht.
Das ist mehr Entdeckung , nämlich dass die zeichnerisch ermittelte Steigung , doch anders ist als die 2 für f(2) bis f(0)

wenn im bild oben bei y = 5 nun 10 wäre , dann wäre die Höhe natürlich 2.8
Komme auf f‘(1) = 1 wenn ich eine tangente einzeichne....
ja , ist ok ................... ein anderer kommt auf 1.1 oder 1.2 oder 0.9 ........... völlig ok bei dieser Fragestellung.
Was ist wenn die Skalierung auf der y Achse doppelt so groß ist wie auf der x Achse?
In dem gezeigten Fall war ja die Steigung 1,4 durch eins. Wenn die Skalierung auf der Y Achse doppelt so groß ist, wäre sie dann 2,8 durch 1?
Danke für die Hillfe!