Wie zeichne ich den Graphen einer Funktion f ,wenn dessen 1. und 2.Ableitung vorgegeben sind?
Schriftlich verstehe ich es einigermaßen,aber zeichnerisch bin ich mir nicht sicher.Unten ist ein Bild der Aufgabe
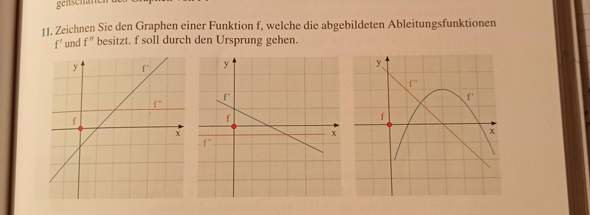
3 Antworten
Ich glaube du sollst hier eher skizzieren anstatt genau zu zeichnen. Du kannst dir zu nutze machen, dass der höchste Exponent pro Ableitung immer um 1 kleiner wird. Z.b bei dem ersten Beispiel weißt du, dass die Steigung konstant größer wird. Beziehe wichtige Punkte wie Nullstellen, Wendestellen und Extremstellen in die Skizze mit ein. Bspw. bei dem ersten Beispiel ist die erste Ableitung eine lineare Funktion, d.h x^1, die zweite Ablietung einfach nur noch eine Konstante. Dementsprechend handelt es sich bei der zweiten Ableitung wahrscheinlich um eine Parabel.
Ich hoffe das hilft. Wenn nicht, stelle ruhig noch mal eine Nachfrage.
bei der ersten Aufgabe ist das eine nach oben geöffnete Parabel mit Scheitelpunkt bei x=1 (y-Wert des Scheitelpunkts ist nicht eindeutig und kann beliebig gewählt werden, bei der Aufgabe aber so, dass f dann durch den Ursprung verläuft)
eine Gerade aufgeleitet ergibt eine Parabel
die Ableitung hat bei x=1 eine Nullstelle mit Vorzeichenwechsel von - nach +, d.h. f hat dann bei x=1 einen Extrempunkt (Tiefpunkt)
dritte Funktion:
Tiefpunkt bei x=1
Hochpunkt bei x=5
Wendepunkt bei x=3
Die Extremstellen der Ursprungsfunktion f(x) sind immer die Nullstellen von f‘(x) und die Wendepunkte von f(x) sind die Extrempunkte von f’(x) und die Nullstellen von f‘‘(x).
Wenn du den Änderungsgraphen einer Funktion zeichnest, dann kannst du immer mit einem Plus die Bereiche des Graphen markieren, in denen der Graph steigt, mit einem Minus die Bereiche, in denen der Graph fällt. Dementsprechend muss der Änderungsgraph bei einer nach unten geöffneten Parabel sich zunächst im positiven Bereich befinden, da f(x) eine positive Steigung hat und nach dem Hochpunkt im negativen (der Graph fällt). Bei der ersten Aufgabe steigt der Graph, befindet sich aber im negativen Bereich und hat eine Nullstelle bei x=1. Daher weißt du, dass die Ursprungsfunktion bis zum Extrempunkt fällt und danach wieder steigt, es sich also um eine nach oben geöffnete Parabel handeln muss.
Merk dir also: Ist f‘(x) vor der Nullstelle negativ und nach der Nullstelle positiv, liegt ein Tiefpunkt vor, umgekehrt ein Hochpunkt. Da sich beim Ableiten der Grad der Funktion immer um eins verringert, kannst du anhand der Parabel in der letzten Abbildung z.B. ableiten, dass es sich bei der Ursprungsfunktion um eine ganzrationale Funktion dritten Grades handelt. Diese hat zwei Extrempunkte, da f‘(x) zwei Nullstellen aufweist. Erst wechselt das Vorzeichen von negativ zu positiv, daher hat man zuerst einen Tiefpunkt, da sich die Funktion zuerst im negativen Bereich befindet, f(x) zu Beginn also eine negative Steigung hat. Zwischen den beiden Extrempunkte hat man dann den Wendepunkt bei x=3. Den Hochpunkt also bei x=1 und den Tiefpunkt bei x=5.