Wie sieht eine Polynomfunktion 3. Grades aus, die keine Extremstellen hat?

Schon die simple Funktion

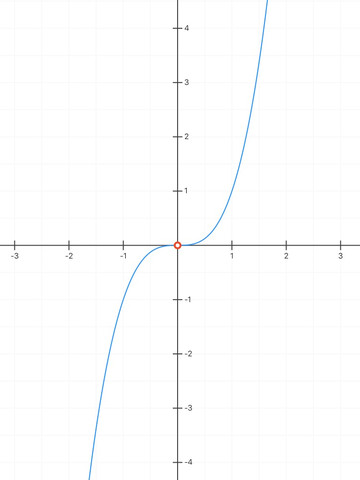
f(x) = x³

hat keine Extremstelle. Die einzige „Kandidatin“ x=0 ist keine, da dort zwar die Ableitung

f'(x) = 3x²

den Wert 0 annimmt, was jedoch keine hinreichende Bedingung für eine Extremstelle darstellt. Die Ableitung wechselt dort nämlich nicht das Vorzeichen. Allerdings hat f'(x) an dieser Stelle ein Minimum (nämlich 0), was x=0 zu einer Wendestelle von f(x) macht.

Neben dem einfachen x³ kann es noch sein, dass die anderen beiden dritten Wurzeln imaginär sind.  

f(x) = x³ + 9x              in Linearfaktoren: x(x²+ 9)

So zum Beispiel, f(x) = x³.

So:

https://de.wikipedia.org/wiki/Sattelpunkt