Wie rechne ich die Kreiszahl Pi aus nach Achimedes?
Ich schreibe meine Facharbeit über die Kreiszahl Pi und als selbständige Aufgabe muss ich die Kreiszahl Pi ausrechnen und dabei habe ich mich entschieden es nach Achimedes zu tuen nur weiss ich nicht wie ich es ausrechnen soll.Ich danke schon mal im Vorraus.
LG
1 Antwort
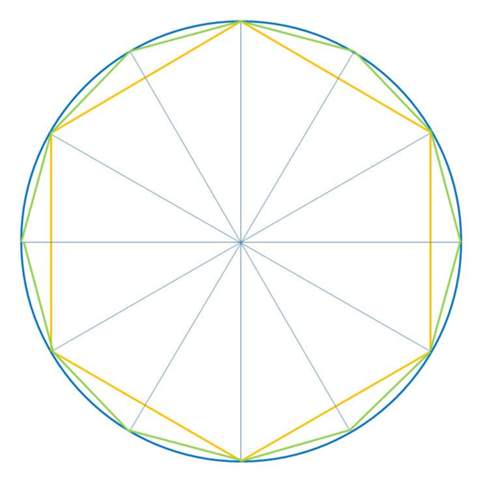
Archimedes entwickelte eine Methode, in der er sich über den Einheitskreis an Pi annäherte. Der Einheitskreis hat den Radius 1 und Pi lässt sich, wie bekannt durch die Formel „Umfang geteilt durch Durchmesser (U / D)“ berechnen. Wir kennen ja in unserem Fall das D, da der Einheitskreis den Radius 1 hat, heißt D = 2. Archimedws hat also außerhalb des Kreises ein regelmäßiges Sechseck gezeichnet. Dabei erkennt man, dass der Umfang des äußeren 6-Eckes größer als der Kreis ist, der des inneren aber kleiner. Die Seitenlängen dieses 6-Eckes sind jeweils 1. Archimdes teilte nun die Seiten der beiden 6-Ecke und zeichnete ein 12-Eck, dann ein 24-Eck usw. So näherte er sich Stück für Stück dem Umfang des Einheitskreises, also Pi, an.
Na steht da doch. Wie er auf die Idee gekommen ist, dass es da eine Zahl gibt, die das Verhältnis des Umfangs eines Kreises zu seinem Durchmesser angibt, weiß ich allerdings nicht. Glaube, das wird nur Archimedes wissen, falls sowas nicht überliefert ist.
Okay Dankeschön
wird es heute genauso gerechnet? Wenn nein was sind die Unterschiede und könntest du das erklären?
bin mir nämlich ziemlich unsicher
Also Archimedes war circa 250 v. Chr. der erste, der mit dem 96 Eck versucht hat, Pi zu berechnen.
Andere Rekorde bei der Berechnung von Pi kamen zum Beispiel von Liu Hui, der nach 263, Pi mit fünf Dezimalstellen und der Methode des 3072 Eck berechnet hat.
Andere Methoden, die bekannt sind, um sich der Zahl Pi anzunähern, sind zum Beispiel die Monte Carlo Simulation. Die Monte Carlo Simulation ist ein Verfahren aus der Stochastik, die ungefähr so verläuft:
Die Kreiszahl Pi wird mit der Montecarlo Methode angenähert, bestimmt, durch das vierfache der Wahrscheinlichkeit, mit der ein innerhalb des Quadrat zufällig gewählter Punkt In den Kreisabschnitt fällt.
Aufgrund des Gesetzes der großen Zahlen sinkt mit steigender Anzahl von Experimenten die Varianz des Ergebnisses und nähert sich so an PI an.
Diese Methode ist bekannt, jedoch nicht besonders aktuell.
Heutige Rekorde bei der Berechnung von Pi, stammen zum Beispiel von Fabrice Bellard, der mithilfe einer Software und der Chudnovsky Formel, die Zahl Pi 2010 auf ca 2.699.999.990.000 Dezimalstellen berechnen konnte. Durch seine eigene Formel wurde diese Berechnung anschließend von Shigeru Kondo und Alexander Yee im Jahr 2011 verifiziert.
Der neueste Rekord für die Berechnung von PI stammt aber vom Google LC aus dem Jahr 2022, womit man mithilfe der Berechnung durch die Y-cruncher Software und der Chudnovsky Formel, die Zahl Pi auf 100.000.000.000.000 Dezimalstellen berechnen konnte.
Vielen Dank. Weisst du vllt mehr über die Berechnung von 2022 denn dann würde ich es als Vergleich nehemen z.b Was die untscheide beim rechnen sind usw. Weisst du auch wie es gerechnet wurde also genauer?
Derzeit werden der bereits erwähnte Chudnowsky-Algorithmus (https://de.wikipedia.org/wiki/Chudnovsky-Algorithmus) aus dem Jahr 1988, und die Y-Cruncher Software (https://de.wikipedia.org/wiki/Y-cruncher) verwendet. Bin leider kein Profi in Sachen IT, am besten liest du dir einfach mal durch, was diese beiden Dinge sind, glaube dort wird es besser erklärt, als ich das kann.
Trotzdem Vielen Danke.
Hast du vllt eine Idee was ich für eine Fragestellung nehmen könnte für meine Facharbeit. In meiner Facharbeit geht es um Die Kreiszahl Pi von früher nach Achimedes und von Heute aber mich fehlt eine Fragestellung und mir fällt nichts ein.
Oh Gott, leider glaube ich nicht, dir da eine große Hilfe sein zu können, da ich mich wahrscheinlich nicht so gut in dein Umfeld, in welchem du diese Arbeit schreibst, hineinversetzen kann. Allerdings fände ich, bzgl. deiner Schilderung, Fragen, wie zb. ob die Methoden von früher, hinsichtlich der heutigen Technik, wirklich unpräziser waren oder sonstiges in der Art, interessant. Allerdings, weiß ich nicht, wie schon gesagt, unter welchen Umständen und vor allem zu welchem Zweck du deine Arbeit schreibst, weshalb ich der Meinung bin, dass du immer noch die beste Person bist, um eine Fragestellung für deine Arbeit zu finden :)
Wie kam er aber darauf? Weisst du es?