Wie leitet man graphisch eine lineare Funktion ab?
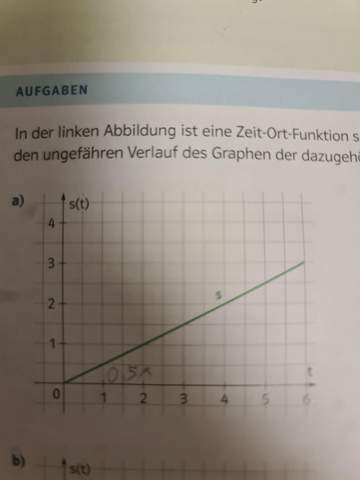
Wie gehe ich da vor, ich weiß nicht wie man zu der Steigung 0,5 gekommen ist und wie der Graph jetzt letztendlich aussieht,bitte helfen
4 Antworten
Mögliche Steigungsdreiecke
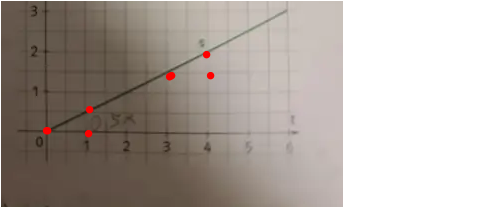
führen zu einer Steigung von 0.5
Da die Gerade überall gleich steigt , ist die Steigung überall 0.5
Der Graph ist also eine waagrechte zur x - Achse durch (0/0.5)
.
Weil die Veränderung in der Zeit - Ort - Funktion überall gleich ist , erkennt man das eine konstante Geschwindigkeit v vorliegt . Diese v stellt die Waagrechte dar .
v ist die Ableitung ( Steigung ) des Weges nach der Zeit.
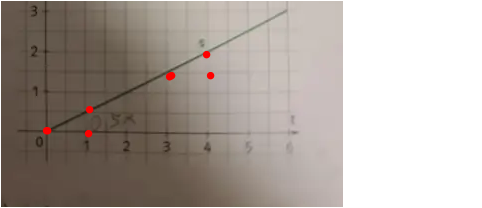
f(x)= 0,5x
Die bekommst du mithilfe des Steigungsdreieck raus. Das wendest du so an. Du gehst von dem Schnittpunkt auf der y-Achse (in diesem Fall 0) eins nach rechts. Dann schaust du, wie viel cm du hoch musst, bis du die Gerade triffst. Hier musst du 0,5 cm hoch, weshalb du 0,5x hast.
Also wenn du damit meinst, eine Gerade bei dem y Wert von 0,5 parallel zur x-Achse zu zeichnen
Mit Steigungsdreieck die Steigung ermitten, dann eine waagerechte Gerade (also eine Gerade, die parallel zur x-Achse ist) auf y-Höhe dieses berechneten Wertes zeichnen.
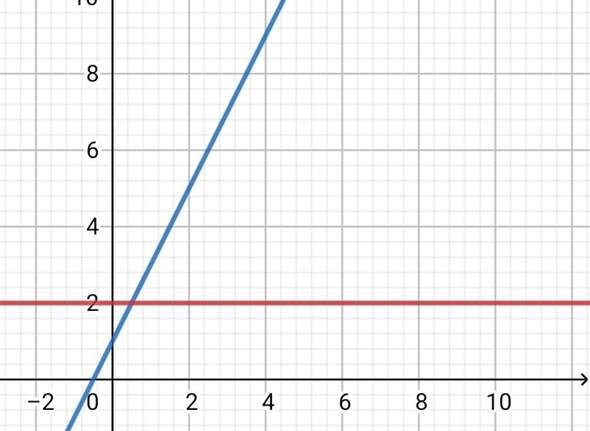
Hier ein Beispiel:
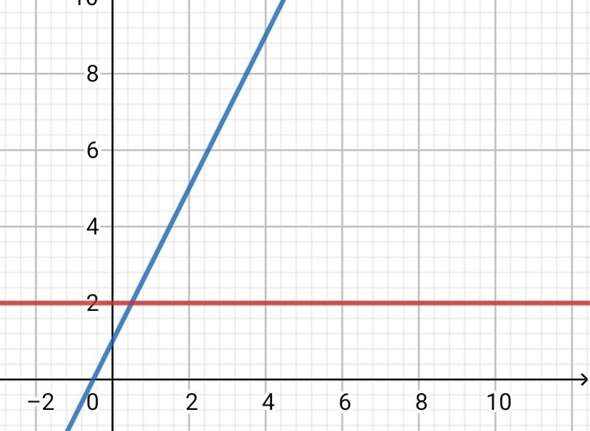
Der rote Graph ist die Ableitungsfunktion. Die Steigung des blauen Graphens ist Zwei, deswegen ist die Ableitung Zwei.
Gerne :)
Steigungsdreieck sollte dir bekannt sein.
Ja aber was mach ich mit dieser Steigung jetzt? warum ist die Ableitung dann waagrecht
Die Ableitung beschreibt die Steigung. Wenn die immer gleich ist, ist deren Graph eine Parallele zur x-Achse, da es ja immer der gleiche Steigungswert ist.
Vielen Dank, und dann den Graph von 0.5 auf der y Achse aus zeichen?