Wie leite ich von Geschwindigkeit und Zeit nach der Beschleunigung ab?
Hallo liebe Leute!
Ich verzweifle an folgender Aufgabenstellung:
Bei einem mathematischen Pendel hängt an einem Faden ein kleiner Körper mit vernachlässigbarer Ausdehnung. Die Geschwindigkeit dieses Massenpunktes wird durch die Beziehung v(t) = 0,25 m/s * sin(3,14 s^−1 t) in der Zeitspanne 0 < t < 1s beschrieben. Wie lautet der Ausdruck für die Beschleunigung des Punktes?
Ich weiß, dass a=dv/dt ist, aber wie setze ich das ein und wie leite ich ab? Mir sind die einzelnen Rechenschritte irgendwie nicht klar :(
2 Antworten
a = dv(t)/dt richtig :)
d( 0,25 m/s * sin( 3,14^(-t) ) / dt
Nun heißt es innere mal äußere Ableitung
Die Ableitung des sin ist der cos
Das schwierige ist jetzt
3,14^(-t)
abzuleiten
Dafür lohnt sich ein Blick in eine Ableitungstabelle:
http://www.frustfrei-lernen.de/mathematik/ableitung-tabelle-formelsammlung-mathematik.html
= -1 * ln(3,14) * 3,14^(-t)
Jetzt müssen noch beide Schritte zusammengeführt werden:
a(t) = -0,25 * ln(3,14) * 3,14^(-t) * cos( 3,14^(-t) )
-- Alle Berechnungen ohne Gewähr --
Ja das wäre in dem Falle richtig.
Leider war das für mich etwas schwierig zu erkennen.
Lösungsvorschlag - siehe Bild
Im Gegensatz zu Deinem Beispiel startet mein Pendel nicht in der negativen, sondern in der positiven Umkehrlage. Deine Lösung erhältst Du analog zu meinem Lösungsvorschlag.
Gruß, H.
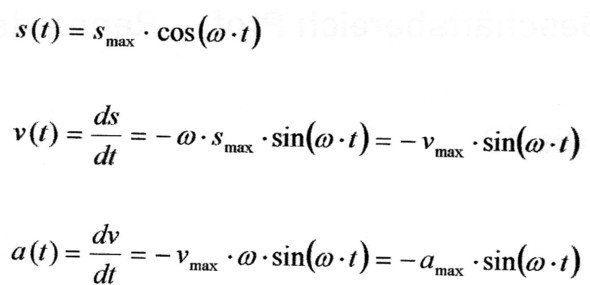
Tippfehler!
In der letzten Zeile handelt es sich nicht um die Sinusfunktion, sondern um die Cosinusfunktion. sorry
Das schwierige ist jetzt 3,14^(-t) abzuleiten
Dafür lohnt sich ein Blick in eine Ableitungstabelle:
Denke das soll 3,14 (also pi) s^-1 (Einheit) mal t heißen.
Damit wäre das Argument im sinus auch dimensionslos.