Wie kann ich diese Matheaufgabe Lösen? Planimetrie?
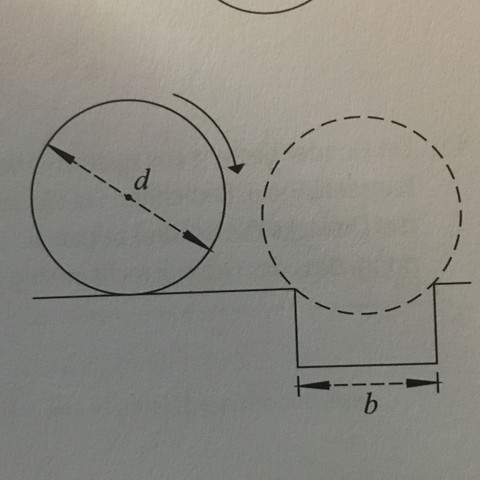
Wie löse ich diese Aufgabe? Die Kugel mit Durchmesser d rollt in den Graben breite b wie tief sinkt sie ein?
Die Lösung ist
h=1/2(d-[d^2-b^2])
Die eckigen Klammern sollten eine Wurzel sein!
Danke!
4 Antworten
du hast doch schon die Lösung ???
Mach mal von der Vertiefung durch die Kugel eine waagrechte Linie so dass die Vertiefung zu wäre. Darauf bildeste Senkrechte zum Kreismittelpunkt.
Den Kreismittelpunkt verbindeste dann mit der Kannte wo Kugel in Vertiefung aufliegt.
Nun haste 2 rechtwnkliche Dreiecke. Die Hypothenuse ist Kreisradius die eine Seite die Hälfte von b
Bei newcomer fehlt noch was , aber der Weg ist richtig
im dreieck gilt r² = h² + b²
und dieses h mß noch von r abgezogen werden ; daher das minuszeichen in deiner lösung .
und d = 2r , also r = d/2
kann es sein, dass man 2 quadrate macht, eines mit seitenlänge d und eines mit b, deren flächeninhalt voneinander abzieht, die wurzel zieht um die seitenlänge eines weiteren quadrates zu bekommen, wobei man dann d minus diese seitenlänge mal 0.5 rechnet, um h zu bekommen?
nur ein versuch, sorry wenns falsch ist
Hallo Barui
Newcomer und Halbrecht haben schon das Wesentliche gesagt. Ich fasse es nur noch einmal zusammen.
Du verlängerst als erstes die waagrechte Linie, auf der die Kugel ursprünglich lag, über den Graben hinweg. Dann zeichnest du vom Mittelpunkt M der im Graben ruhenden Kugel eine senkrechte Linie nach unten bis an den Kugelrand. Den Schnittpunkt mit dem Kugelrand (Kreis) bezeichnest du mit S, den Schnittpunkt (Fußpunkt) mit der waagrechten Linie über den Graben bezeichnest du mit F. Eine der Grabenkanten, auf denen die Kugel aufliegt bezeichnest du mit A.
Den Kugelradius nennst du r, wobei gilt r = d/2. Die Strecke von M bis F nennst du x, die Strecke von F bis S nennst du t. t ist die Tiefe, um die die Kugel im Graben eingesunken ist.
Nun siehst du, dass gilt t = r - x. Wir brauchen also noch x. Das errechnest du aus dem rechtwinkligen Dreieck AFM. Es gilt nämlich (Pythagoras) r² = (b/2)² + x². Daraus folgt x² = r² - (b/2)² und weiter x = Wurzel(r² - (b/2)²).
Somit ist t = r - x = r - Wurzel(r² - (b/2)²) = d/2 - Wurzel((d/2)² - (b/2)²) =
= (1/2)(d - Wurzel(d² - b²)).
Es grüßt HEWKLDOe.
x = h
und HEWKLDOe hat auch (b/2)^2 geschrieben anstatt b² (hatte Halbrecht falsch)
r^2 = h^2 +(b/2)^2