Wie ist arctan definiert?
Hallo, ich möchte arctan(x) ableiten. Leider weiß ich nicht, wie arctan definiert ist. Ich weiß nur, dass tan (x) = sin(x) / cos(x)
Kann mir einer sagen , was arctan(x) mit Termen aus sin und cos ist? Taylorpolynome -reihen hatte ich nämlich noch nicht. Danke im Voraus.
Des Weiteren möchte ich fragen, ob mir jmd. sagen kann warum arctan(0) = 0 ist
3 Antworten
Vereinfacht gesagt: arctan ist die Umkehrfunktion von tan. Wenn also f(x) = tan(x) ist, dann ist f^(-1) (x) = arctan(x).
("Vereinfacht gesagt" deshalb, weil man bei tan erstmal den Definitionsbereich einschränken muss, damit tan überhaupt eine Umkehrfunktion hat.)
Es gilt immer f (f^(-1) (x) ) = x. Demnach ist arctan(0) ein Wert, den man in tan einsetzen kann, um wieder 0 herauszubekommen. Also: tan( arctan(0) ) = 0.
Schau auch mal auf dieser Seite, wenn sie nicht zu kompliziert ist:
https://de.wikipedia.org/wiki/Arkustangens_und_Arkuskotangens
Ich weiß gar nicht, ob es überhaupt eine geschlossene Formel für arctan gibt, die nur mit sin und cos auskommt. arctan wird ja recht kompliziert als Umkehrfunktion definiert.
Die Ableitung von arctan kann allerdings trotzdem berechnet werden und wird oft in Tabellen angegeben: https://www.mathe-online.at/mathint/diff1/i_beweisinvWfun.html
Nutz aus, dass gilt:
Kettenregel ergibt:
Danke für die Antwort. Mir ist etwas unklar, wie man auf 1+tan^2 kommt. Hast du eine Formel für den arctan(x) für mich? Damit ich mir die Herleiten kann zum besseren Verständnis. Denke es ist 1/cos^2(x), oder?
Es ist (tan(x))' = 1/cos²(x) und es ist (sin(x)²+cos²(x))/cos²(x)) = sin(x)²/cos²(x) + cos²(x)/cos²(x) = tan²(x) + 1 q.e.d
Es später viel einfacher, diese Umformung anzuwenden.
Übrigens, dieser "Trick" funktioniert mit jeder Funktion, die sich eindeutig umkehren lässt.
Herleitung der Formel:
Es gilt(falls f bijektiv ist)
f(f^(-1)(x)) = x I Differenzieren
f'(f^(-1)(x))*f'^(-1)(x)) = 1 <=> f'^(-1)(x) = 1/f'(f^(-1)(x))
Eine Umschreibung vom arctan(x) mithilfe von Sinus und Kosinus ist mir nicht bekannt, aber als Taylorreihe.
Willst du's nur wissen oder selber herleiten?
Hast du hier schon geschaut?
https://www.mathelounge.de/90085/ableitung-arctan-x-1-1-x-2-herleiten-und-d-dx-ln-cosh-x-sinh-x
Und zum zweiten Teil der Frage:
Überleg doch, wie tan geometrisch definiert ist!
Gegenkathete durch Ankathete.
Wenn die Gegenkathete null ist (tan = 0), muss auch der Winkel null sein, logo, oder?
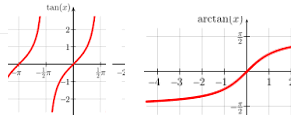
Beide Funktionen (tan und arctan) gehen also durch den Nullpunkt:
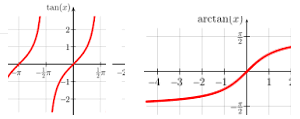
Oder hilft das?
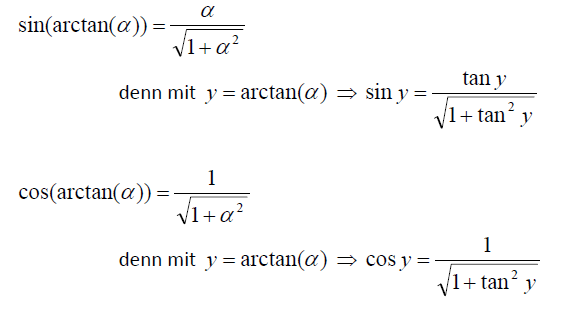
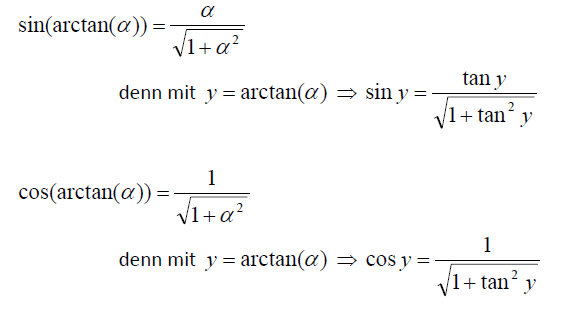
Danke für die Antwort! Wie ich sehe, ist dann also die Ableitung von arctan(x) = 1/(1+(arctan(y)^2)), oder? Das mit der Herleitung hat mir geholfen. Mir geht es vor allem darum, den Arctan allgemein herzuleiten und dann vom Tangens die Herleitung zum arctan herzuleiten. Den zweiten Teil hab ich nun dank dir.
Ja, so ungefähr, aber die Ableitung von arctan(x) ist dann einfach 1/(1+x^2)
Da ist keine Winkelfunktion mehr drin.
Da schwurbelt einer, wie's geht:
https://www.youtube.com/watch?v=eXtIXxGX34c
oder hier (gibt noch Teil 1 und 3):
Danke für die Antwort, leider ist auf Wikipedia der arctan nur mit Taylorpolynomen definiert. Deswegen frage ich, was der arctan als sinus/cosinus kombination oder als feststehende Formel ist, um es ableiten zu können. z.B. tan(x) = sin(x)/cos(x).