Wie hoch ist die Wahrscheinlichkeit, dass bei wöchentlicher Ziehung innerhalb von 100 Jahren mindestens einmal dieselben Lottozahlen gezogen werden?
Ich habe gerade eine alte Frage gesehen und mitbekommen, dass das bereits zweimal geschehen ist. Ich selbst bin Mathematiker, aber kein Statistiker - daher hätte ich die Wahrscheinlichkeit fast bei 0 gesehen und hiermit nicht gerechnet…
7 Antworten
Ohne jetzt eine Rechnung machen zu wollen (ich HASSE Wahrscheinlichkeitstheorie und Statistik), aber das ist nur eine andere Ausprägung des
https://de.m.wikipedia.org/wiki/Geburtstagsparadoxon
Es ist daher nicht überraschend wenn da ein (im Verhältnis zur Wahrscheinlichkeit für einen Lottogewinn) recht hoher Wert heraus kommt.
Vielleicht geht das hier?
https://matheguru.com/stochastik/geburtstagsproblem.html?utm_content=cmp-true
Vielen Dank - das ist genau das, was ich suche! Wenn ich das richtig interpretiere, ist die gesuchte Wahrscheinlichkeit dann gegeben durch P(A), wobei die „Anzahl der Tage im Jahr“ der Anzahl (49 über 6) der möglichen Kombinationen im Lotto und die Anzahl k der Personen k = 5.200 der Anzahl der Ziehungen in 100 Jahren entspricht… Muss mal ausrechnen, was dabei rauskommt… :-)
Die Wahrscheinlichkeit, dass sich eine Lotto-Zahlenreihe innerhalb von 100 Jahren mindestens einmal wiederholt, entspricht der Wahrscheinlichkeit, dass eine bestimme Zahlenreihe mindestens zweimal gezogen wird.
n = 5200 (Anzahl der Ziehungen)
p = 1 : 15537573
(a) p(0 Erfolge) = (5200 über 0) * p^0 * (1-p)^n = 0.999665383382588
(b) p(1 Erfolg) = (5200 über 1) * p^1 * (1-p)^(n-1) = 0.000334560637504332
Wahrscheinlichkeit für mindestens 2 Erfolge =
1 - (a) - (b) = 0.0000000559799080769889
Das entspricht einer Wahrscheinlichkeit von 1 : 17863552, ist also wie zu erwarten geringer als die Wahrscheinlichkeit bei einer einzigen Ziehung 6 Richtige zu haben.
"entspricht der Wahrscheinlichkeit, dass eine bestimme Zahlenreihe mindestens zweimal gezogen wird"
Es entspricht der WK, dass *irgendeine* Reihe doppelt vorkommt. Da liegt auch der Fehler in deiner Rechnung.
Siehe Geburtstagsparadoxon.
Mit der WK von einem Erfolg hast du bereits eine Dopplung gefunden.
Sozusagen die erste Folge wählen und dann versuchen sie nochmal zu ziehen, also einmalig im Lotto zu gewinnen
> aber auch das wäre noch eine Unterschätzung der WK denn man muss ja nicht die erste Folge treffen sondern kann jede beliebige bereits dagewesene Folge treffen.
Das Problem ist im Übrigen nicht binomialverteilt
1 zu 2987 in etwa.
Die Wahrscheinlichkeit für 6 Richtige ist 1 zu 15.537.537.
Mein Ansatz als Nicht Mathematiker.
Wenn jede Ziehung exakt einmal vorkommt in 15537537 Ziehungen, dauert es die Zeit bis die ersten Zahlen wieder dran kommen.
15537537/ 52 Wochen = 300 Tausend Jahre etwas.
Geteilt durch 100 Jahre = 2987
Von daher ist die Wahrscheinlichkeit dass es in 100 Jahren passiert der Kehrwert. Also 1 zu 2987 ist etwas ,0.00003347
Dir ist vermutlich klar, dass das die tatsächliche WK massiv unterschätzt
Dass während den ersten 15 Millionen Ziehungen nicht wenigstens eine Dopplung vorkommt ist sehr unwahrscheinlich.
Schon nach der Hälfte der Ziehungen besteht für jede weitere Ziehung *jeweils* eine Chance von > 50% eine Dopplung zu erhalten
Bei mehr als 5 mio Ziehungen mit > 50% chance kein Erfolg ist praktisch unmöglich
Die Wahrscheinlichkeit dafür müsste sich folgendermaßen berechnen lassen:
1-(1398315/13983816 * 1398314/13983816 * 1398313/13983816 * .... ) wobei die Zahl der Multiplikationen in der Klammer der Anzahl der Ziehungen entspricht die bis heute stattgefunden haben. Die Zahl vor der Division bleibt innerhalb des Terms 2X gleich, da es 2X eine doppelte Ziehung gab und bei dieser Ziehung der Pool der möglichen Ziehungen nicht zugenommen hat. Die Wahrscheinlichkeit, dass eine exakte Kombination drankommt, die irgendwann schonmal kam nimmt aufgrund der konstant steigenden Zahl der Kombinationen mit jeder Ziehung zu. Aktuell gab es bis heute ca. 6000 Lottoziehungen, was bedeutet, dass bei jeder Ziehung derzeit eine Chance von etwa 0,048% besteht, dass es eine erneut Dopplung einer früheren Lottoziehung gibt. Und eine gute 75% Chance (geschätzt), dass das bis heute schon mindestens 1X aufgetreten ist. Bei 100 Ziehungen pro Jahr passiert das derzeit alle 22 Jahre statistisch gesehen. Bis in 60 Jahren müsste sich dieser Wert nochmal verdoppeln. Dann wird das durchschnittlich alle 11 Jahre passieren...
13983815 meinte ich natürlich und es ist bei 6000 Ziehungen keine 0,048% Chance, sondern eher eine 0,043% Chance... Rest sollte aber stimmen
Ich bin selbst nicht gut in Statistik aber ich habe mal Wolfram Alpha befragt.
Rechnung über die Gegenwahrscheinlichkeit "nur unterschiedliche". Dazu gibt es bei der ersten Ziehung (49 über 6) Möglichleiten, dann wöchentlich eine weniger. Insgesamt 52 Wochen.
Hier kulant geschätzt:
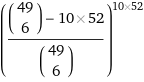
=~ 0,98
Also ohne Superzahl ist die Chance < 2%.
Allerdings dürfte 52 Lottoziehungen pro Jahr weit unterschätzt sein (weltweit).
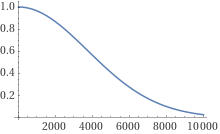
Hier wie es für 1000 Ziehungen aussieht ohne Superzahl, dafür weniger kulant geschätzt
(Die große Zahl ist 49 über 6)
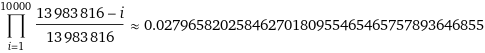
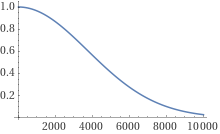
Also für 1000 pro Jahr ca 97% Chance für mindestens eine Dopplung.
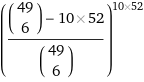
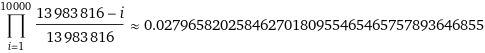
Ich kann Wikipedia leider nicht öffnen, da ich zur Zeit in China bin - Google ist dort auch gesperrt, sonst hätte ich schon selbst versucht, das rauszubekommen… :-) Ich wollte nur mal checken, ob 2 Ereignisse in etwa 65 Jahren Lottogeschichte bereits hochsignifikant sind. Trotzdem vielen Dank!