Wie berechne ich die reelle (und komplexe) Partialbruchzerlegung von dem folgenden Therm?
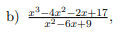
Ich dachte man müsste bei p(x) eine Polynomendivision durchführen, da der Grad von P ja größer ist als der von Q aber ich finde durch erraten keine Nullstelle... kann mir bitte jemand weiterhelfen? bzw. welches Verfahren muss ich verwenden um den Zählergrad zu verringern?
desweiten frage ich mich ob man hier nur die reelle oder auch die komplexe Partialbruchzerlegung bestimmen kann ( ich denke nicht aber bin mir nicht sicher)
mfg
2 Antworten
Mache die Polynomdivision und Du erhältst einen Restbruch, auf den Du die Partialbruchzerlegung anwenden kannst:
PD => =x + 2 + (x-1)/(x-3)²
die ausgespuckte Nullstelle ist -1,879
Die Nullstellen des Zählers sind doch uninteressant! Der Nenner wird ja in seine Nullstellen "aufgesplittet".
In Deinem Fall hättest Du nach der Polynomdivision des Zählers durch (x+1,879) als Bruch:
(x+1,879)(x²-...)/(x-3)². Wie soll es denn dann weitergehen?
Übrigens muss als Rest 0 rauskommen, wenn Du ein Polynom durch seine Nullstelle teilst. Du musst natürlich mit dem exakten Wert der Nullstelle rechnen, bzw. je genauer desto geringer ist der Rest (aufgrund der Nullstellenrundung).
verstehe nicht durch welchen Therm ich dividieren soll, wenn nicht durch (x - (nullstelle))
Du dividierst einfach den Zählerterm durch den Nennerterm. Hier ist ja der Zählergrad größer als der Nennergrad, d. h. Du hast einen unechten Bruch. D. h. man kann ihn (wie bei Zahlen auch) in einen "ganzen Anteil" + Restbruch aufsplitten. Dieser Restbruch ist dann ein echter Bruch auf den Du die Partialbruchzerlegung anwenden kannst.
Der Zählergrad ist größer als der Nennergrad, und deshalb ist eine Partialbruchzerlegung nicht möglich.
https://www.arndt-bruenner.de/mathe/scripts/partialbruchzerlegung.htm
gibt es keinen Weg den Grad des Zählers zu verringern? Empfohlen wurde mir die Polynomdivision, Ausklammern usw.
Irgend eine Möglichkeit muss es ja geben sonst wäre das ja eine sehr schlechte Übungsaufgabe dafür
Ja, gibt es.
Und wenn du die Webseite benutzt hättest, die ich dir gepostet habe, dann hättest du jetzt auch das Ergebnis der Polynomdivision :
(x^3 - 4x^2 - 2x + 17) / (x^2 - 6x + 9) = x + 2 + (x - 1) / (x^2 - 6x + 9)
Hier noch mal eine andere Webseite :
https://www.arndt-bruenner.de/mathe/scripts/polynomdivision.htm
hatte ich eigentlich auch versucht, aber der erst Schritt ist doch eine Nullstelle zu erraten richtig? Ich hab das mit -5 bis 5 probiert und dann einen Online Rechner benutzt der mit als Nullstelle ausspuckt, wenn ich das in die Funktion (p) einsetze kommt aber auch nicht 0 raus...