Warum ist eine Matrizenmultiplikation nicht kommutativ?
Hat jemand eine schlüssige Erklärung?
6 Antworten
Weil es Gegenbeispiele gibt. Beispielsweise:
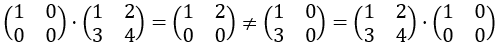
Und naja. Es verwundert mich auch nicht, da ja bei der einen Matrix quasi die Zeilen und für die andere Matrix quasi die Spalten verwendet werden. Und wenn man dann die beiden Matrizen vertauscht, wird auch geändert, ob man die Spalten oder die Zeilen der jeweiligen Matrix verwendet.
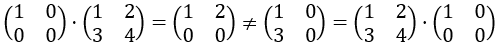
Aber klar. Nimm dir zwei Matrizen A und B (es reichen 2x2) mit allgemeinen Elementen. Schreibe einmal AB und einmal BA hin und berechne. Dann wirst du sehen dass dies im Allgemeinen zu unterschiedlichen Termen für die neue Matrix führt.
Nehmen wir mal den einfachsten Fall von 2 Dimensionen: spezielle Matrizen können Spiegelungen und Drehungen darstellen.
Wenn wir den Punkt (1,0) an der y-Achse spiegeln, erhalten wir (-1,0). Wenn wir danach um 90 Grad gegen den Uhrzeigersinn drehen, landen wir bei (0,-1).
Jetzt sehen wir uns das in umgekehrter Reihenfolge an: wenn wir (1,0) nehmen und um 90 Grad gegen den Uhrzeigersinn drehen, haben wir (0,1). Wenn wir danach an der y-Achse spiegeln, bleiben wir aber bei (0,1), denn der Punkt liegt auf der y-Achse. Um wie im ersten Fall bei (0,-1) zu stehen, hätten wir an der x-Achse spiegeln müssen.
Also ist diese Matrixmultiplikation nicht kommutativ.
Wiel du, wenn ich mich recht erinnere ja zeile mit spalte Multiplizierst.
Haste also eien MAtritze A und eine Matritze B
Mulptiplizierst du ja die Zeilen von A mit den Spalten von B
Wenn du die aber vertauschst.
Multiplizierst du die Zeilen von B mit den Spalten von A.
Was ja eine ganze andere rechnung ist.
Imgrunde müsstest du beide Matritzen wenn du sie tauschst um 90 grad rotieren. Dann haste das gleiche ergebniss.
Kann man einfach mit einem Beispiel widerlegen. Eine geometrische Erklärung kenne ich nicht. Manchmal kommt es auch mit der Anzahl der Zeilen/Spalten schon nicht hin.