Vorzeichenwechsel-Kriterium?
Ich habe verstanden wie man bei einer Funktion den Tief oder Hochpunkt berechnet, aber leider weiß ich nicht wie ich die extremstellen bestimmen soll weil keine Funktion vorhanden ist. Wie bestimmte ich denn die extremstellen im Intervall?
2 Antworten
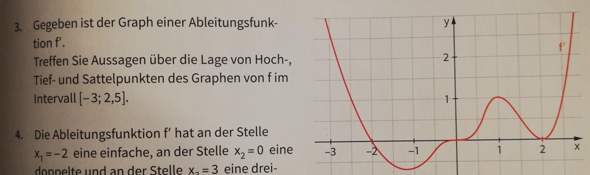
1) f'(-2) in der Skizze für f' ( 1. Abgleitung) ist offenbar gleich 0, also ein Extrempunkt von f, weil: die 2. Ableitung von f ist hier in der Skizze die 1. Ableitung von f' also die Steigung von f', ist negativ bei (-2 ; 0 ), somit ist (-2 ; 0 ) ein Hochpunkt von f
2) ....
usw.
also ich meine (-2 ; y) ist ein Hochpunkt von f (nicht (-2 ; 0 )), der Wert von y ist natürlich noch zu bestimmen
habe vergessen dass in der Fragestellung steht: Vorzeichenwechselkriterium, aber sonst könnte ich genauso fragen Wieso machst du das mit Vorzeichenwechsel, wenn man das schon an der Steigung (entspricht in der f' - Skizze der 2. Ableitung) direkt sehen kann?
Bist du Hellseher, dass du weist, das ich bei x=0 Probleme bekomme? ;-)
f'(0) ist 0 weswegen das Kriterium der 2. Ableitung nicht hilft.
Besser gesagt bei 2 von 3 stellen ist die zweite Ableitung 0, du hast die einzige Stelle benutzt, wo das Kriterium was taugt
Ich habe einfach links beim 1. Punkt begonnen (wie bereits gesagt, hatte ich vergessen: Vorzeichenwechselkriterium in der Fragestellung), um dann den Fragesteller anzuhalten, es bei den nächsten Punkten selbst zu versuchen, vielleicht hätte ich das Vorzeichenwechselkriterium bei den anderen Punten auch angewandt, aber selbstverständlich taugt mein Kriterium der Betrachung der höheren Ableitungen (Geradheit oder Ungeradheit der Ableitungen höherer Ordnung ungleich Null) auch, auch wenn man nur eine Skizze vorliegen hat.
Also Zuerst brauchst du die Notwendige Bedingung für Extremstellen: die erste Ableitung ist 0.
Du suchst die also alle stellen raus, wo die Ableitungsfunktion 0 ist. Das sind die Punkte die Potentiell eine Extremstelle sind.
Als nächstes benutzt du das Hinreichende Kriterium des Vorzeichenwechsel:
Wenn die Ableitung an dieser Stelle das Vorzeichen Wechselt (also kurz davor negativ und kurz danach positiv oder umgekehrt) dann hast du dort eine Extremstelle.
Es gilt: Wechsel von positiv nach negativ => Maximum
Wechsel von negativ nach Positiv => Minimum.
Z.b ist bei x=2 weder Minimum Noch Maximum, da die Funktion da die Achse nur berührt, es gibt somit kein Vorzeichenwechsel.
Bei x=-2 ist hingegen ein Maximum
genau , die Abl zeigt wohl einen Sattelpunkt und das ist dann "bloss" eine Extremstelle ? Ok .
so weit konnte ich die fkt finden , und weil sie 7ten grades ist habe ich mir die Nachprüfung gespart .
https://www.wolframalpha.com/input/?i=f%28x%29+%3D+%28x-2%29%28x-2%29%28x%2B2%29*x%C2%B3*1%2F3*
Das Vorzeichenkriterium reicht aus:
an x=0 wird das Vorzeichen gewechselt, also ist es eine Extremstelle, sogar ein Minimum denn:
Kurz davor ist die Ableitung negativ, also fällt sie
Kurz danach positiv, also steigt sie
Wieso machst du das mit der zweiten Ableitung, wenn man das schon am Vorzeichenwechsel direkt sehen kann?
Außerdem hättest du dann bei x=0 Probleme