Verstehe ich das richtig, dass man die CH3 und H-Atome die an den beiden C Atomen mit Doppelbindung dran sind jeweils um die Achse zu den C Atomen drehen kann?
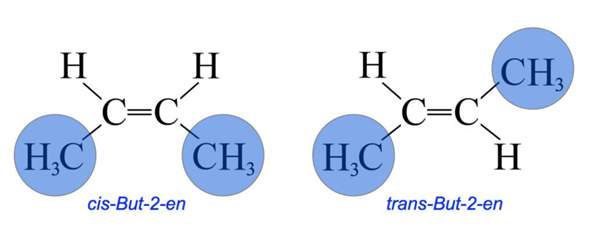
Also die Drehbarkeit ist exakt um die Achse, die die CH3 und H-Atome mit den beiden C-Atomen in der Mitte (die mit Doppelbindung) verbindet, richtig?
Und dies ist ein Fall der KONFIGURATIONSisomerie und NICHT der Konformationsisomerie, weil durch Drehung an den Einfachbindungen KEINE Gleichheit der beiden Moleküle erreicht werden kann, richtig?
Wenn man durch Drehung um Einfachmoleküle Gleichheit der Moleküle erreicht, jhandelt es sich immer um Konformationsisomerie, aber nicht um Konfigurationsisomerie, richtig?
Und eine letzte Frage:
Kann es passieren, dass es ausreicht nur eine Valenzstrichformel wie oben von zwei Moleküle zu sehen, um zu beurteilen, ob Konformationsisomerie vorliegt? Ich denke, Konformationsisomerie kann man nie aus einer Valenzstrichformel sicher ableiten? Weil man einfach nicht weiß, welche Atome in die Blatt Eben hineingehen und welche rauszeigen.
ABER man kann Konfigurationsisomerie von Valenzstrichformeln ableiten, richtig? Weil man auch in der Valenzstrichformel sehen kann, we die Atome ungefähr angeordnet sind, sodass man einen sicheren räumlichen Unterschied sehen kann und somit Konfigurationsisomerie vorliegt und wenn man zum Beispiel eine Doppelbindung hat kann je nach Fall diese Information reichen um ausschließen zu können, dass durch Drehung um Einfachbindungen die Moleküle Gleichheit erreichen und somit keine Konformationsisomerie vorliegen kann (wie im obigen Beispiel mit Buten)?
1 Antwort
Verstehe ich das richtig, dass man die CH3 und H-Atome die an den beiden C Atomen mit Doppelbindung dran sind jeweils um die Achse zu den C Atomen drehen kann?
Ja, das ist richtig. Entlang einer Einfachbindungen ist eine Drehung immer möglich. Dadurch ändert sich an den cis-trans-Isomeren genau nichts.
Und dies ist ein Fall der KONFIGURATIONSisomerie und NICHT der Konformationsisomerie, weil durch Drehung an den Einfachbindungen KEINE Gleichheit der beiden Moleküle erreicht werden kann, richtig?
Ja, das ist korrekt.
Wenn man durch Drehung um Einfachmoleküle Gleichheit der Moleküle erreicht, jhandelt es sich immer um Konformationsisomerie, aber nicht um Konfigurationsisomerie, richtig?
Ja richtig. Konformere sind letztlich nur mögliche Molekülgeometrien, bei denen alle Bindungen bestehen bleiben und wo es dabei durch gewisse geometrische Konstellationen zu bevorzugten Stellungen kommt. Die sind aber nicht stabil, sondern nur eine energetisch bevorzugte Konstellation. Drehbarkeit eben.