Unterschied Reihen und Parallelkompensation?
Hallo Zusammen
Ich habe auch nochmal eine Frage zur Reihen-/Parallelkompensation
Ich habe eine Parallelschaltung von 3 Motoren am 230v Netz
Strom ist gegeben cos phi ist gegeben Parallelkompensation habe ich wie folgt gemacht:
Blindleistungen Graphisch addiert und als probe nochmal mit komplexen Zahlen addiert
Gesamtblindleistung Vorzeichen gedreht und C ausgerechnet
Nun soll ich in Reihe kompensieren?
Ich kenne das bisher nur von einer Duo-Schaltung bei Leuchtstoffröhren hier wird das Doppelte überkompensiert.
Wie funktioniert das bei drei Induktiven Verbrauchern?
Blindleistung linear addieren und dann doppelt kompensieren?
Ich bräuchte mal einen Rechenansatz
Ich habe extra keine Werte angegeben weil ich es selbst rechnen möchte
Vielen dank für eure Hilfe
P.Manns
4 Antworten
Die induktive Last kann man modellieren als Serienschaltung L und R (hier 100 Ohm, 200mH - nur als Beispiel).
Blindleistungskompensation:
Der Kondensator C in Serie kompensiert die Spannung an der Last-Induktivität.
Somit ist die Phasenverschiebung zwischen Strom und Gesamtspannung null.
Du kannst die hierfür notwendige Bedingung so anschreiben:
Sowohl Z wie auch der Winkel sind durch die Last vorgegeben. Somit weißt du alles, und kannst C berechnen.
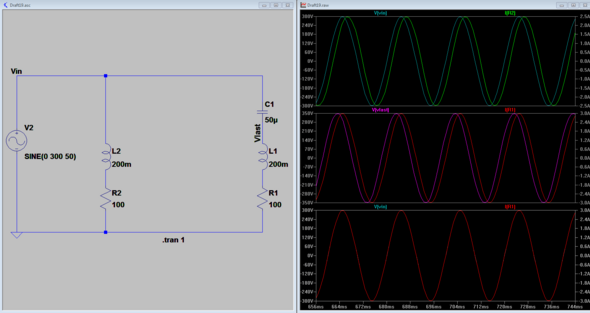
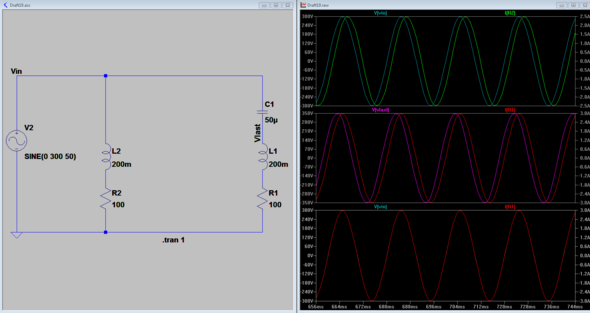
Im Bild sind die Verhältnisse an der unkompensierten (links) und kompensierten (rechts) Schaltung gezeigt:
- Ganz oben im Graphen siehst Du U und I für den unkompensierten Fall: also hat man hier eine Phasenverschiebung von etwa 30°.
- Im mittleren Graphen siehst Du die Spannung an der Last Ulast und den Strom: hier hast Du natürlich die gleiche Phasenverschiebung.
- Ganz unten siehst Du die Gesamtspannung und den Strom: hier hast du keine Phasenverschiebung, da C gemäß obiger Bestimmungsgleichung gewählt wurde.
Allerdings ist die Spannung an der Last (350V) nun größer als die Spannung der Quelle (300V), da ja auch am Kondensator eine Spannung abfallen muss. Das nennt man Resonanzüberhöhung.
Du kannst auf diese Weise nicht erreichen, dass die Spannung an der Last gleich bleibt - wie auch? Deshalb wird diese Art der Kompensation auch nur selten verwendet.
Wenn du bei gegebenem cos φ und Z mit einem seriellen C auf ein bestimmtes neues cos φ' kompensieren willst, gibt es zwei Lösungen für C:
Für cos φ'=1 ist das wiederum die obige Formel.
Deine Lösung kann ich jetzt nicht nachvollziehen. Vielleicht verstehe ich deine Notation aber falsch.
Die doppelte Kompensation an der Leuchtstofflampe deshalb, weil nur eine von beiden kompensiert wird, so dass die Gesamtkompensation für beide Lampen zusammen wieder passt (die zweite bleibt ja "unkompensiert" bzw. wird von der doppelt kompensierten mitkompensiert). Das macht man nur, damit man die Phasenverschiebung durch den Kondensator zusätzlich dafür nutzen kann, dass die Leuchtmittel zeitversetzt leuchten, so dass der Stroposkopeffekt unterdrückt wird. Gleichzeitig sind beide Leuchtstofflampen zusammen nur "einfach" kompensiert. Also eine hat positives cosPhi, die andere einen ähnlichen negativen cosPhi. Ich hoffe, das ist zu verstehen, wie ich das meine^^.
Man kann die beiden Leuchtstofflampen durchaus auch einfach kompensieren, aber dann fehlt die Unterdrückung des Stropo-Effekts). Wenn du eine ungerade Anzahl Leuchtstofflampen hast, darf diejenige, die keinen Partner hat, ebenfalls nur einfach kompensiert werden.
Dieser Zeitversatz wird in deinem Fall nicht benötigt. Also entweder einmal an zentraler Stelle auf den Gesamt-cosPhi kompensieren oder jeden Motor einzeln.
Die Gesamtkompensation ist nur sinnvoll, wenn die drei Motoren immer gemeinsam laufen. Sonst musst du einzeln kompensieren.
Also Blindleistungen zusammenaddieren und dann einmal kompensieren (aber nicht exakt auf cosPhi=1 bringen, weil Motorwicklung+Kondensator=Schwingkreis und bei cosPhi=1 hättest du Resonanz. Daher ein bisschen über- oder unterkompensieren, so dass der kompensierte cosPhi, sofern in der Rechenaufgabe nichts anderes angegeben, bei ca. 0.95 liegt). Evtl. dabeischreiben, warum du nicht auf 1 kompensiert hast, damit du vllt. noch einen Pluspunkt abgreifst.
Wie das konkret gerechnet wird, haben andere bereits geschrieben :-).
Der Serienkondensator muss den Phasenwinkel φ der induktiven Last (drei Motoren) kompensieren, also bei gegebenem Strom I durch die Last und einer Lastspannung UL muss
Die Spannung an der Last ist dann aber nicht die Netzspannung, sondern etwas größer.
Hallo michiwien22
danke für die schnelle Antwort
eine Frage bleibt aber noch
Ich habe weder UC noch C gegeben d.h. I und UL müssen die werte vor der Kompensation sein oder?
Da der Widerstand von C rein kapazitiv ist bleibt I ja gleich.
Wie sieht es mit UL aus ?
LG P.Manns
Viel Dank für die ausführliche Antwort
Und wenn ich nicht nach cos(φ)=1 sondern beliebig kompensieren will
Z.B: nach cos(φ)=0,9 muss mann es so rechnen oder ?
C = 1/(ω Z sin φ) - 1/(ω Z sin (cos^-1(0,9))
obwohl wenn ich hier zu probe (auf cos(φ)=1) einsetzte
C = 1/(ω Z sin φ) - 1/(ω Z sin (cos^-1(1)) = C = 1/(ω Z sin φ) - 1/0 !
also eher
C = 1/(ω Z sin φ) - 1/(ω Z sin (cos^-1(1-0,9))
denn dann bei Probe (auf cos(φ)=1)
C = 1/(ω Z sin φ) - 1/(ω Z sin (cos^-1(1-1)) = C = 1/(ω Z sin φ) - 0