Stochastikaufgabe -Lotto!?
ich habe noch eine Aufgabe, bei der ich leider nicht weiterkommen
Lotto heißt auch "6 aus 49". Beim Lotto werden sechs Kugeln gezogen.
a) Wie viel verschiedene Ziehungen sind möglich? Begründen Sie,dass P("sechs Richtige") (ungefähr gleich- Zeichen) 7* 10 ^-8 ist.
b) Berechnen Sie die Wahrscheinlichkeit dafür, drei Richtige zu erzielen. (als Orientierungshilfe: Bei drei Richtigen hat man zufällig drei der sechs Zahlen richtig getippt und die anderen drei ...)
Danke im Vorraus für eure tolle Hilfe ;)
2 Antworten
Bei dieser Aufgabe handelt es sich um eine Hypergeometrische Verteilung. Beim Lotto handelt es sich um eine Stichprobe ohne Zurücklegen, wobei die Versuche nicht stochastisch unabhängig sind, deswegen hat man für solche Fälle das Lotto Modell bzw. eine Hypergeometrische Verteilung eingeführt : (siehe Bild)
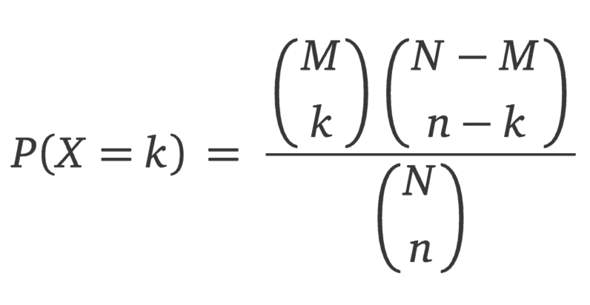
Wobei P= Wahrscheinlichkeit
X =Zufallsgröße
N= die Anzahl der Elemente in der Grundgesamtheit(Bei Lotto=49, da es 49 Kugeln gibt)
M = die Anzahl der Elemente, die für uns günstig sind(quasi wie viele richtige)
n= die größe der Stichprobe(wie oft wir ziehen (6mal))
k= die Anzahl der Elemente aus M, die in n enthalten sind. (Von 6 zahlen müssen k richtig sein)
Als Beispiel Aufgabe b)
N=49
M=6, da es 6 richtige Zahlen gibt
n=6, da wir 6mal ziehen
k=3, da wir 3 Richtige ziehen wollen
Jetzt nur noch oben einsetzen und ausrechnen.
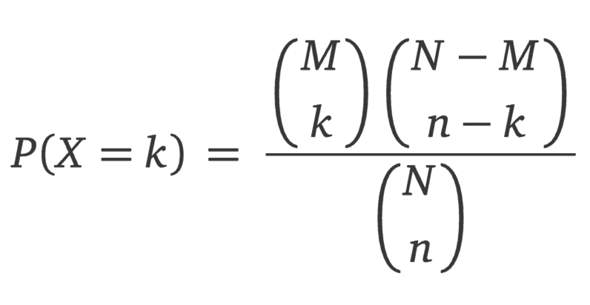
vielen Dank! Weißt du auch wie ich a) berechnen kann?
Guck mal, hier wird das ganz gut erklärt:
https://de.wikibooks.org/wiki/Mathematik_f%C3%BCr_Sch%C3%BCler/_Stochastik/_Lotto