Stimmt meine Rechnung zum kreuzprodukt?

Ist mein Ergebnis richtig?
5 Antworten
Das kannst du selbst prüfen. Skalarprodukte mit dem Normalenvektor müssen 0 sein.
In der Mitte hast du: 0*1-(-2)*4=8, d. h. (4 8 -3) ist die korrekte Lösung.
Du musst dir das Schema "irgendwie" einprägen...
Schaue mal hier - da wird weiter unten mit einer kleinen Hilfestellung gezeigt wie man sich das relativ leicht berechnen kann (indem man die ersten beiden Zeilen nochmal drunter setzt und dann über Kreuz multipliziert und subtrahiert): https://studyflix.de/mathematik/kreuzprodukt-vektorprodukt-2254
Du kannst ja selbst Überprüfung, ob es stimmt. Wenn du 2 Vektoren im Vektorprodukt (Kreuzprodukt) im R^3 nimmst bekommst du ein Vektor der senkrecht auf den anderen steht. Also das Standartskalarprodukt ist null. Also rechnest du Probe:
also hast du dich verechnet.
Ich habe mir das immer so aufgeschrieben, dass die erste Komponente jeweils noch einmal unter der letzten Komponente des Vektors steht. Dann geht es Schritt für Schritt über Kreuz.

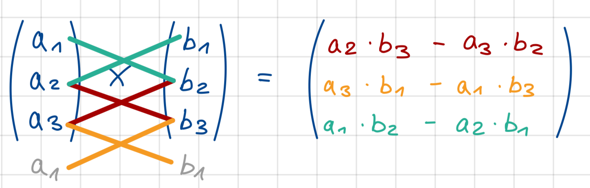
Ne ist falsch

Du musst einfach in die Formel einsetzen. Dann ergibt sich für die zweite Koordinate (0*1)-(-2*4)
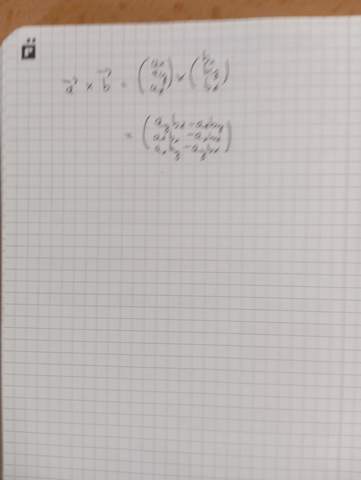
Kannst du mir bitte deine Rechnung schicken? Würde mich sehr freuen
Danke. Weiß du auch wieso? Versuche das Thema zu verstehen