Standardabweichung einer Normalverteilung berechnen - ohne Tabelle?
Ich würde gerne die Standardabweichung bei gegebener Wahrscheinlichkeit und Erwartungswert berechnen. Die Wahrscheinlichkeit beträgt 0.995 und der Erwartungswert ist 2.5 mm.
Mit Tabelle würde ich 0.995 in der Tabelle suchen, Zeile und Spalte ablesen und somit den Wert u herausbekommen und die Standardabweichung berechnen.
Jetzt ist die Frage wie ich die Standardabweichung ohne Tabelle und mit dem Taschenrechner berechne (Modell TI-nspire CX CAS). Ich habe eine Möglichkeit gefunden u auszurechnen, jedoch dauert das eintippen und berechnen etwas lange. (bild1) Der NormCdf-befehl funktioniert anscheinend nicht mit solve nicht. (bild2)
Habt ihr eine bessere Lösung?
(die Aufgabe (c): https://aufgabenpool.srdp.at/bhs/download.php?qid=749&file=Magneten.pdf)
L.G.
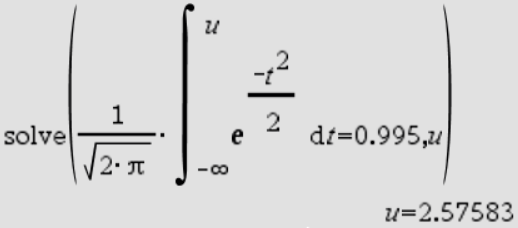

2 Antworten
TI-83/TI-84 haben eine Funktion invNorm. Diese liefert
invNorm(.995) = 2.575829303
Ich bin mir sicher, dass der TI-nspire CX CAS auch eine solche Funktion besitzt.
Ich kenne mich mit TI-Rechnern nicht wirklich gut aus, aber vielleicht geht es, wenn man den Rechner anweist, es numerisch zu lösen (nSolve statt solve und eine Toleranz mitgeben):
nSolve(normCdf(2.4,2.6,2.5,x)=.995,x,.001)
Danke es hat funktioniert. Ich bekomme jedoch 0.03562 statt 0.03822 (wie in der Lösung) heraus. Hängt das mit der Toleranz zusammen?
Die untere Grenze (2.4) ist natürlich falsch. Es muss -∞ sein. ich weiß aber nicht, ob und wie man das bei einem TI-Rechner eingeben kann:
nSolve(normCdf(-∞,2.6,2.5,x)=.995,x,.001)
Ich habe eine bessere Möglichkeit gefunden, um u auszurechnen. (siehe bild3)

Danke für die Antwort! So geht es natürlich leichter ;) Hast du zufällig eine Idee wie man die Standardabweichung direkt berechnen könnte? (sowie im pdf bei den Lösungen)