Wie ist die Stammfunktion von Wurzel von 4x?
Ich bin am verzweifeln ich hab alles probiert aber irgendwie mach ich das falsch :/ Also meine frage ist einfach wie die Stammfunktion von f(x)=Wurzel(4x) ist Danke für eure Hilfe :))
2 Antworten
Ohne die Integrationsregeln für Wurzeln zu verwenden, kannst du es als Exponentenform umschreiben.
√(4 x) = (4 x)^(1/2)
Das ganze Integrieren:
∫(4 x)^(1/2) dx = ∫ 2 * x^(1/2) dx = 2 * 2/3 x^(3/2) + c = 4/3 * x^3/2 + c = 4/3* √(x^3) + c
Die vereinfachung von x^3/2 zu √(x^3) gilt nur für x >= 0, das ist durch die Definitionsmenge von f(x) aber schon gegeben.
Also... Wenn wir davon ausgehen, dass Wurzel aus 4x eigentlich 2*x hoch 1/2 ist(also zwei mal wurzel x), dann kommt man mit der der Aufleitungsformel x hoch n+1 geteilt durch n+1 im Nenner auf 2 x hoch 1/2 +1 und im Zähler auf 1/2 + 1.
Daraus ergibt sich: 2mal dritte wurzel aus x geteilt durch 3/2. Brüche werden dividiert indem man mit dem Kehrbruch multipliziert: Also ergibt sich: 2mal dritte wurzel aus x mal 2/3
Das Ergebnis lautet also: 4mal dritte Wurzel aus x geteilt durch 3 + c (Integrationskonstante) (oder: vier Drittel mal dritte Wurzel aus x plus die Integrationskonstante)...
Ich hoffe, ich konnte helfen...
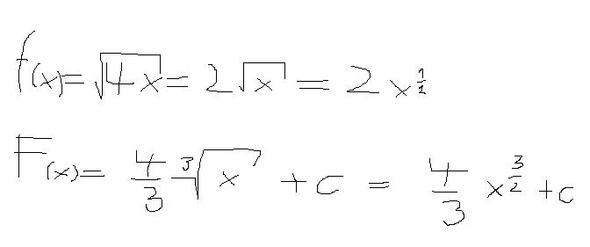
Du bist aufs richtige Ergebnis gekommen, hast aber zwei Fehler gemacht, die sich Gegenseitig negiert haben ;)
In deiner Stammfunktion steht Dritte Wurzel aus x = x^3/2, das stimmt aber nicht. Die dritte Wurzel aus x ist x^1/3, und x^3/2 ist die Quadrat-Wurzel aus x^3.
eine frage und zwar wie kommst du von ∫(4 x)^(1/2) dx auf∫ 2 * x^(1/2) dx ? diesen schritt kann ich nicht nachvollziehen :/ aber schon mal danke für deine Hilfe :)