Wie kann ich Sinus- und Kosinuswerte abschätzen?
Wie kann man sin(1) ungefähr mit dem Einheitskreis abschätzen? Sin (1°) ist ja fast 0, aber was ist mit sin(1)
2 Antworten
Wenn man Pi als 3 nähert, dann entsprechen 90° (=pi/2) etwa 1,5 rad.
Somit entspricht 1 rad etwa 60°.
Der genaue Wert von sin(60°) lässt sich aus der Wertetabelle ablesen:
Die Genauigkeit sollte für einfache graphische Skizzen ausreichen.
Aber warum enstpricht 1 rad 60° ?
Weil (1 rad / 2*pi rad) * 360° ~= 57,3° ~= 60°
Du berechnest mit
1/360 * 2pi (rad) = 0,0175...
den Radiant von 1°.
Betrachtet man die Reihenentwicklung von sin():
sin(x) = x/1! - x^3/3! + x^5/5! + O(x^7)
und ignoriert den Teil O(x^7), dann ergeben die drei ersten Summanden:
h(x) = x/20(1/6 * x^4 - 10/3 * x^2 + 20)
###
sin(1) ~ 0.8414709848079
h(1) ~ 0.841666...
Der Fehlerbetrag beläuft sich auf nur ~ 0.000195681
Wie man an den folgenden Graphen erkennen kann, passt sich h(x) im Intervall [-π/2,+π/2] dem sin(x) "sehr gut" an.
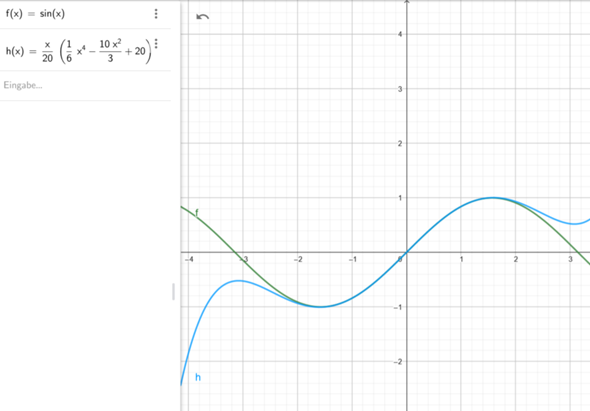
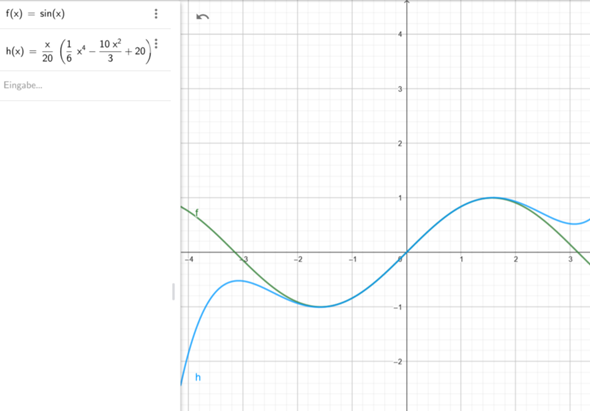
Aber warum enstpricht 1 rad 60° ?
Die formel ist doch 1/360 ×2 pi , also ungefähr 0,0175