Schwierigstes Matherätsel?
Ich spreche an diese Person meine Ehre aus die diese Aufgabe lösen kann!
Viel Spaß. Ich musste in den Lösungen nachschauen. Wenn jemand eine Ergebnis reinschreibt sage ich ob es richtig ist oder nicht;)
4 Antworten
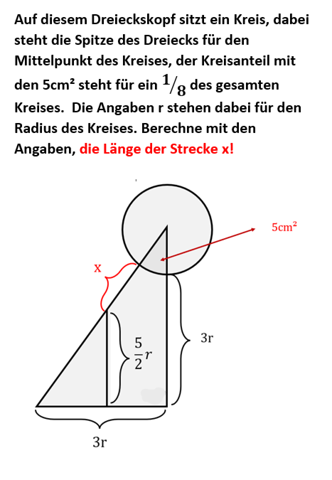
Die Katheten sind 3r und 4r lang, d. h. die Hypotenuse ist 5r.
Strahlensatz:
5r:(4r) = (4r-x):(5/2r) <=> 5/4 * (5/2r) = 4r-x <=> 25r/8 =4r-x <=> x=4r-25r/8=7/8r
U=8*5cm²=40 cm²=pi*r² => r=Wurzel(40/pi)
also x=7/8 * Wurzel(40/pi), um ganz genau zu sein...
Ups, da war ich wohl etwas zu voreilig, habe mich auf mein (mäßiges) Augenmaß verlassen und "losgelegt" ohne über dieses kleine Detail nachzudenken...
auf die 45° bin ich auch nur zufällig aufmerksam geworden : Ich dachte , schreib mal erst alles hin , was man so an Fakten rausholen kann .
Und da man bei GF ja mit Gleichschenkelig geimpft wird , merkte ich auf
x = 2,107 cm
Hallo,
die Aufgabe enthält eine böse Falle.
Die Skizze wirkt, als sei das Dreieck rechtwinklig. Das kann aber nicht sein. Wenn der Winkel oben ein Achtel des Kreises herausschneidet, muß er ein Achtel von 360°, also 45° haben.
Dann müßte der dritte Winkel aber auch 45° besitzen und das Dreieck müßte gleichschenklig sein. Das ist es aber nicht, denn der Schenkel, der vom Kreismittelpunkt ausgeht, ist vier Radien lang, der untere nur 3.
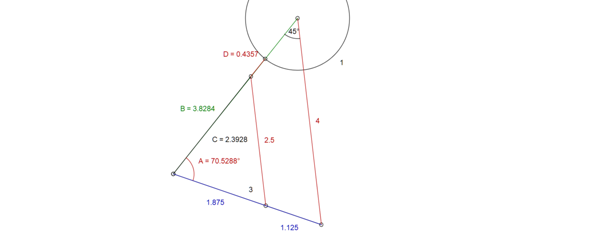
Zunächst muß also über den Sinussatz der Winkel links unten berechnet werden. Sei der Winkel phi.
Dann gilt: sin (phi)/4=sin (45°)/3. Somit ist sin (phi)=0,9428090416 und der dazugehörige Winkel phi ist 70,52877937°.
Da der Winkel zwischen dem unteren Schenkel und der noch unbekannten Seite des Dreiecks bekannt ist, läßt sich diese unbekannte Seite, die von links unten wieder zum Kreismittelpunkt führt und auf der die Strecke x liegt, nach dem Kosinussatz berechnen. Sie ist 3,828427125 Radien lang.
Um den Rest zu lösen, muß vorausgesetzt werden, daß die eingezeichnete Strecke von 2,5 Radien Länge parallel zur Seite rechts liegt, sonst ist die Aufgabe unlösbar.
Ist sie parallel, kommt nun der Strahlensatz zur Anwendung. Dann verhält sich nämlich die Länge der Strecke von der linken unteren Ecke des Dreiecks bis zum Fußpunkt der Parallele zur unteren Seite wie 2,5:4 und ist damit 1,875 Radien lang.
Nun kann man die Strecke von der linken unteren Ecke bis zum unteren Anfang der Strecke x berechnen: Nennen wir ihn y, dann gilt nach dem Strahlensatz:
y/3,828427125=1,875/3 und damit y=2,392766953 Radien.
x ist dann 3,828427125-2,392766953-1=0,4356601718 Radien lang.
Wenn 5 cm² ein Achtel der Kreisfläche sind, ist die Kreisfläche 40 cm² groß und damit r die Wurzel aus (40/pi)=3,568248232 cm lang.
Somit ist x=0,4356601718*3,568248232=1,554543638 cm lang.
Siehe auch die Konstruktion (Zahlen in Radien):
Herzliche Grüße,
Willy
kleine Bildersuche im Netz ergab bei mir keine Treffer . So bekannt ist dieses Verwirrteil evtl nicht.
Qualle wäre interessant
Ja. Ist auf jeden Fall schlampig gemacht, denn die angegebene Lösung paßt nicht zu den angegebenen Maßen.
radius kreis aus
8*5 = pi * r²
.
winkel im Kreis ist 1/8 * 360 = 45 °
.
Damit wäre das Dreieck gleichschenkelig . Sieht aber überhaupt nicht danach aus.
Denn 3r ungleich 3r+1r
.
1/8 kann nicht stimmen
Das Dreieck kann nicht rechtwinklig sein, wenn der Winkel beim Kreismittelpunkt 45° hat, sonst müßte es gleichschenklig sein. Das ist es aber nicht.