Satz des Thales - Beweis?
Hallo.
Kennt / hat jemand einen Beweis für den Satz des Thales, der nicht "normal" ist, sondern außergewöhnlicher?
Genauso hat es der Lehrer formuliert.
Er verwies, nicht die Seite https://lehrerfortbildung-bw.de/u_matnatech/imp/gym/bp2016/fb1/7_m3_geo/1_hintergrund/2_info/3_thales/#:~:text=%E2%80%9EWenn%20ein%20Dreieck%20rechtwinklig%20ist,%E2%80%9C zu benutzen. Sonst sei die Internetrecherche frei.
Etwas banale Nachfrage: Die 4 Beweise, die in der Wikipedia nachzulesen sind, waren alle 4 bereits Unterrichtsstoff und gelten für die Aufgabenstellung als die 'normalen' Beweise?
Er meinte, die sollen wir a) nicht benutzen und die seien uns zu hoch...
Darf man den (historisch jüngeren) Satz des PYTHAGORAS benutzen?
Jep.
Vektorrechnung? Skalarprodukt?
(Das Skalarprodukt zweier Vektoren ist nämlich 0, wenn sie orthogonal zueinander sind).
Das haben wir noch nicht so richtig behandelt. ABer wenn du es (gut) erklärst, wäre es sicher okay...
Es wird nicht ganz einfach sein, einen Beweis zu finden, der weder in dem von Dir verlinkten Lehrermaterial noch im Wikipedia-Artikel auftaucht.
Trotzdem wäre es toll!
2 Antworten
Hallo diecooleperson1,
im Moment fällt mir nur ein, wie man die Umkehrung des Satzes des Thales auf ungewöhnliche Weise beweisen könnte:
Umkehrung des Satzes des ThalesIst ein Dreieck rechtwinklig, so liegt der Punkt C, an dem der Rechte Winkel liegt, auf einem Kreis um den Mittelpunkt M der Hypotenuse, dessen Durchmesser diese ist.
Wir legen nicht M in den Ursprung eines Koordinatensystems, sondern C, und zwar natürlich so, dass die Katheten entlang der Achsen liegen. Die Länge der Hypotenuse liegt fest.
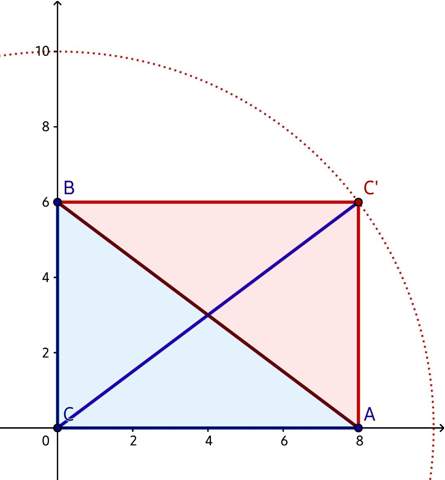
Nun kann man das rechtwinklige Dreieck zum Rechteck ergänzen, und die Verbindung zwischen C und dem diagonal gegenüberliegenden "neuen" Punkt C' ist genauso lang wie die Hypotenuse.
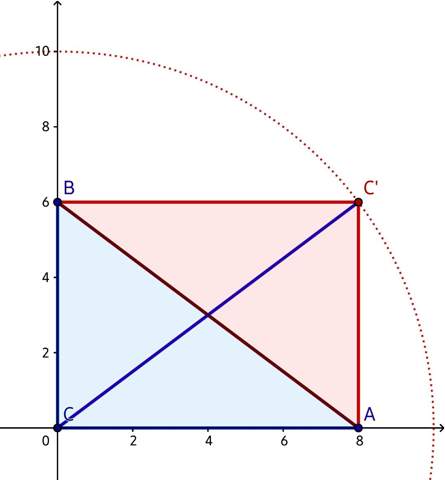
Abb. 1: Die Diagonalen des Rechtecks schneiden sich in M. Dessen Abstand von C ist immer genau die Hälfte der Hypotenusenlänge.
Satz des Thales mit VektorenVektoren sind mathematische Größen mit Richtung in einem mehrdimensionalen Raum, die sich untereinander addieren und mit Zahlen multiplizieren lassen.
Sie lassen sich durch geordnete Paare, Tripel ... von Zahlen darstellen, den Komponenten, ähnlich wie Punkte durch Koordinaten (das hängt eng zusammen).
Anschaulich ist jeder Vektor eine Klasse von Pfeilen gleicher Richtung und gleicher Richtung. Ein einzelner Pfeil heißt ein Repräsentant des Vektors. Ein solcher Repräsentant vom Ursprung bis zu einem bestimmten Punkt heißt dessen Ortsvektor.
Das Skalarprodukt zweier Vektoren a› = (ax | ay) und b› = (bx | by),
(1) ‹a∙b› = ax∙bx + ay∙by,
hängt mit dem Winkel zwischen den Vektoren zusammen; ist es 0, sind sie senkrecht zueinander, z.B.
(2) (4 | 3)•(−3 | 4) = 4∙(−3) + 3∙4 = −12 + 12 = 0
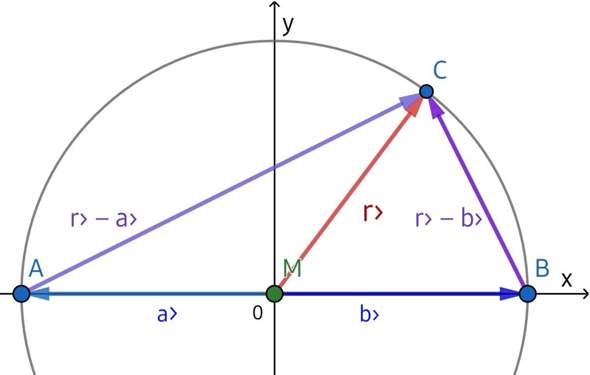
Skalarprodukt gleich 0Wir legen den Mittelpunkt M des Umkreises in den Ursprung und die Seite, die M mittig teilt, auf die x- Achse.
Nach Voraussetzung liegen die Punkte A, B und C gleich weit von M entfernt. Die Entfernung nennen wir r; der Vektor r› = (x | y) ist als Ortsvektor der von C, a› = (−r | 0) der von A und b› = (r | 0) der von B.
Nach PYTHAGORAS ist y = √{r² − x²}.
Von A nach C führt r› − a› = (x + r | √{r² − x²}), von B nach C führt r› − b› = (x − r | √{r² − x²}).
Das Skalarprodukt ist
(3) (x + r)(x − r) + (r² − x²) = x² − r² + r² − x² = 0.
QED
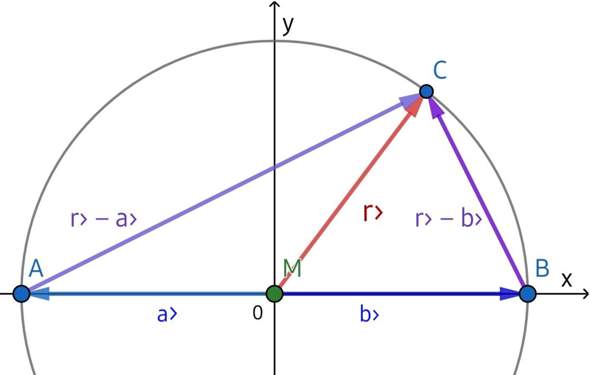
Abb.1: Thales- Dreieck aus Vektoren
Der Satz des Thales ist ein Spezialfall des Kreiswinkelsatzes, der in der Wikipedia elementar bewiesen wird.
Vielen Dank für den Stern für diese Baustelle!