Oktal direkt in Hexadezimal umrechnen
Von Binär oder Dezimal gehts ja recht einfach, aber gibt es eine möglichkeit, eine zahl direkt von oktal- ins hexadezimalsystem, ohne dazwischen ins dezimal- oder binärsystem zu rechnen?
7 Antworten
Von Oktal ins Hexadezimal.
Zum Beispiel (71257305)oct
Hexadezimal rechnen.
Wir rechnen hexadezimal von links nach rechts.
Beginne mit der 7 und verdoppel dreimal in Hexadezimal.
0xE
0x1C
0x38
nächste Ziffer ist 1
0x38+0x1=0x39
Ergebnis dreimal in Hexadezimal verdoppeln.
0x72
0xE4
0x1C8
nächste Ziffer ist 2
0x1C8+0x2=0x1CA
Ergebnis dreimal in Hexadezimal verdoppeln.
0x394
0x728
0xE50
nächste Ziffer ist 5
0xE50+0x5=0xE55
Ergebnis dreimal in Hexadezimal verdoppeln.
0x1CAA
0x3954
0x72A8
nächste Ziffer ist 7
0x72A8+0x7=0x72AF
Ergebnis dreimal in Hexadezimal verdoppeln,
0xE55E
0xCABC
0x39578
nächste Ziffer ist 3 0x39578+0x3=0x3957B Ergebnis dreimal in Hexadezimal verdoppeln.
0x72AF6
0xE55EC
0x1CABD8
nächste Ziffer ist 0
0x1CABD8+0x0=0x1CABD8
Ergebnis dreimal in Hexadezimal verdoppeln.
0x3957B0
0x72AF60
0xE55EC0
letzte Ziffer ist 5
0xE55EC0+0x5=0xE55EC5
(71257305)oct = 0xE55EC5 .
das geht genauso, wie man es auch im dezimalsystem macht.
man macht häufig folgendes:
sei 10010 eine zahl im dualsystem. dann zählen wir 0 * 1 + 1 * 2 + 0 * 4 + 0 * 8 + 1 * 16 = 18
was wir dabei gemacht haben: wir haben, weil wir eben aus gewohnheit im dezimalsystem rechnen die zwischenergebnisse (die einzelnen summanden) bereits im 10er system angegeben bevor wir zusammenzählen.
wollen wir nun das in das oktale system umwandeln rechnen wir wieder im 10er-system:
8^0 = 1, 8^1=0, 8^8=64 , und 64 ist größer als 18, d.h.: wir kümmern uns zuerst um die "8er-stelle" (analog zu 10er-stelle im dezimalsystem). wir rechnen nun 8 * 1 = 8, 8 * 2 = 16, 8 * 3 = 24, und 24 ist bereits zu groß, also haben wir an der 8er-stelle nur eine ziffer 2. dann fehlen uns noch "2" um auf 18 zu kommen. das geht mit einer "2" an der 1er-stelle. => die zahl lautet 22.
all diese rechnungen haben wir aber bereits in einem zahlensystem durchgeführt, nämlich dem 10er-system. das geht aber auch ohne. sowohl das potenzieren als auch das malnehmen lassen sich per definition auf summation zurückführen. und beim addieren von summen addiert man einfach die "ziffern" und guckt, ob man über die grenzen des zahlensystem hinaus-schießt, und damit einen übertrag verzeichnen muss.
beispiel: 7 + 7 = 4 und "1 gemerkt", welches an die nächsthöhere stelle wandert, d.h.: 14
das geht nun auch in allen anderen zahlensystemen. selbes beispiel, also 10010 in dual direkt in oktal:
(dabei gibt es mehrere algorithmen, ich versuche den obigen so genau wie möglich zu kopieren) ich ziehe immer größer werdende 2er-potenzen als dualzahlen von 10010 ab, bis ich gerade noch über der 0 bin. dabei weiß ich aber nicht, ob es diese zahlen in ihrer ziffern-darstellung auch im 8er-system gibt. also spalte ich die zahl in 1er auf. 1 = 1, 2= 1 + 1, 4 = 1+1+1+1 usw.... schnell wird klar, dass der algorithmus nur sinn macht, wenn wir von vornherein nur so lange 1er abziehen und im 8er-system aufaddieren, bis die dualzahl verschwunden ist. schließlich ist ein zahlensystem nichts anderes als eine art und weise die summen von 1+1+1+1...usw anders darzustellen. alle systeme haben eine 1er-stelle.
10010 - 1 = 10011 und 1 gemerkt zum abziehen der nächst-höheren stelle = 10001. im oktalsystem haben wir bereits eine 1. noch ein schritt: 10001 - 1 = 10000. im 8er-system sind wie nun bei 2 angelangt.
das ginge weitaus schneller, wenn wir nicht immer nur "1" abziehen. es ist also sehr sinnvoll zu probieren, ob man nicht auch mal 8 oder z.B.: 20 abziehen kann. z.B.: 8 im dualsystem gleich 1000. ziehe ich das mal ab: 10000 - 1000= 1000. nun muss ich zählen wie viele 1er ich dafür benötigte... das sind nunmal unabhängig davon in welchem system ich dies darstelle 8 mal die 1, oder besser gesagt 1+1+1+1+1+1+1+1. das sind und bleiben "8" in unserem dezimalsystem oder z.B. 20 im 4er-system. die darstellungsart ist egal. es sind "1+1+1+1+1+1+1+1" = zahl vom wert "8" im dezimalsystem. im oktalsystem war ich erst bei 2. nun zähle ich 8mal weiter. und lande bei 3,4,5,6,7,0,1,2, also 2 und "1 gemerkt", also sind wir bei 12. leicht sieht man, dass wir nochmal "8" abziehen müssen, also nochmal "8" im oktalsystem dazu zählen. 3,4,5,6,7,0,1,2 und wieder 1 gemerkt. damit erhalten wir 22.
man rechnet also eigentlich nu mit "plus 1" bzw. "minus 1". man kann aber auch gleich mehrere 1er auf einmal abziehen um alles zu beschleunigen. dafür müssen wir die "anzahl" an 1er aber in worte fassen. dabei müssen wir eine wahl treffen, nämlich "welches system?". da kommt für uns nurdas dezimalsystem in frage, weil wir ständig darin rechnen. hätten wir gelernt im 2er-system zu rechnen, so würden wir nicht erst ins dezimal-system umrechnen.
Da das Umrechnen vom oktal- ins hexadezimalsystem nur eine Umordnung von Dreierbitgruppen in Viererbitgruppen erfordert, ist der Weg über das Binärsystem der Einfachste.
Ohne Wandlung ins dezimal- oder binärsystem geht es wahrscheinlich nicht.
Schon wenn Du das Wort "rechnen" benutzt, hast Du Dich ja auf ein System festgelegt (auch Dein Gehirn ist Hardware)! Da es keinen Rechner gibt, der rein "oktal" rechnet, gibt es auch keine "direkte" Wandlung. Am besten versteht man es, wenn man mit Computersprachen arbeitet, da man:
- schon bei der Ein- und Ausgabe den neutralen Typ "String" verwenden muss
- immer gezwungen wird "typkompatibel" zu arbeiten
- bei mehr als den üblichen 15 (Dezimal-)Stellen gezwungen wird, sich "echte Gedanken für sauberen Algorithmus" zu machen
- leicht die Rechenzeit stoppen kann
Einige Compiler erlauben zwar die begrenzte direkte Eingabe basisfremder Zahlen (0xFF, $F1 usw.), ABER da kümmert sich der Compiler nur einmalig um die Wandlung.
Interessant wäre ABER die Frage:
a) Welches ist der schnellste Algorithmus in ASM (Maschinensprache), der kontinuierlich mindestens 64 stellige okt-Zahlen direkt nach Hex wandeln kann?!
Da gibt es hoch optimierte Befehle wie "Shift Links/rechts" (Schieben aller BIN-Bits um x nach LINKS bedeutet mathematisch 2^x)...
Manchmal ist auch ein scheinbarer Umweg schneller, da einige Befehle weniger Taktzyklen brauchen als andere...
Nur wenn der Nutzen den Aufwand für eine neue Hardware rechtfertigen würde, wäre auch eine 1-Takt-Hardware denkbar... Dafür gibt es aber andere Foren wie FPGA, Mikrocontroller, Assembler...
b) Welches ist der einfachste Algorithmus für einen Menschen mit Papier & Bleistift?
Wenn Du mehr als die üblichen 15 Stellen online wandeln willst (denn bis dahin findet man im Netz hunderte Anfänger-Programme oder "Tools")
siehe http://www.lamprechts.de/gerd/php/RechnerMitUmkehrfunktion.php
Befehl FromBase2Base(x=Argument zum Wandeln, y=Quellbasis, z=Zielbasis)
(intern rechnet der immer nach Dezimal um, da Quell- & Zielbasis hier variabel sind)
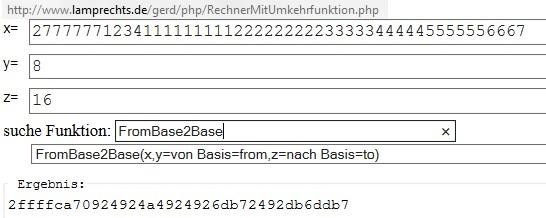
Wie Du im Bild siehst, werden aus 49 Zeichen später 37.
Da der Bruch 49/37 nicht teilbar ist (Periode 324), kann man sich auch nicht einzelne Zeichen herauspicken und direkt wandeln, sondern kommt um eine "Komplettwandlung" (Dreierbitgruppen in Viererbitgruppen also mindestens Binär) nicht herum!
Auch wenn die Frage schon vier Jahre alt ist: Man kann zwar theoretisch die Zahl ohne Umweg direkt vom Oktal ins Hex-System umrechnen, aber mit dem Umweg über das Binärsystem geht es doch wesentlich einfacher.
Ich nehm einfach mal die Zahl, die Hexbaumfall genommen hat. 71257305 im Oktalsystem. Für jede Ziffer im Oktalsystem gibt es eine dreistellige Zahlenkombination im Binärsystem. Das kann man ohne rechnen direkt übersetzen.
7 1 2 5 7 3 0 5
111 001 010 101 111 011 000 101
Die Binärziffern in Dreierblocks kann man jetzt so aufteilen, dass die Ziffern immer in Viererblocks stehen und kann sie dann wieder ohne rechnen ins Hex-System übersetzen.
1110 0101 0101 1110 1100 0101
E 5 5 E C 5
Das geht meiner Meinung nach deutlich einfacher, als dieses ewig lange rumgerechne.