Nullstellen einer Gleichung mit komplexen und konjugiert komplexen Zahlen?
Hallo!
Seit einiger Zeit hänge ich jetzt an einem Beispiel. Ein ähnliches Beispiel habe ich bereits gelöst. Aber durch das Vorkommen einer konjugiert komplexen Zahl (ist ja nicht mehr a + bi sondern a -bi) und dem Betrag (Wurzel(a^2+b^2)) komme ich nicht mehr weiter und würde mich über einen verständlichen Lösungsweg sehr freuen!
Die Angabe wäre wie folgt: Ermitteln Sie alle z aus den komplexen Zahlen, die folgende Gleichung erfüllen.
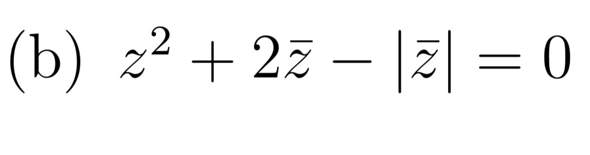
Vielen Dank für jede Hilfe!
LG
2 Antworten
(ist ja nicht mehr a + bi sondern a -bi) und dem Betrag (Wurzel(a^2+b^2)) komme ich nicht mehr weiter
Und?
Setze alles ein und setze Imaginärteil und Realteil getrennt auf 0. (Insbesondere der Imaginärteil bringt schon starke EInschränkungen der Lösungsmenge)
Also: schreib deinen bisherigen Rechenweg hier an, dann helfe ich dir weiter.

Um nun weiter aufzulösen, würde ich mit einer Fallunterscheidung weitermachen...

Demnach erhält man dann weiter...
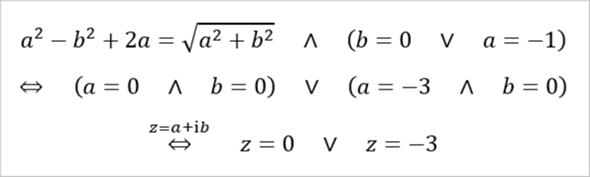
Die Gleichung hat demnach die beiden Lösungen z = 0 bzw. z = -3, falls ich mich nicht verrechnet habe.
=============
Edit: Ich habe gemerkt, dass ich beim Schritt von der zweiten zur dritten Zeile einen Vorzeichenfehler habe.


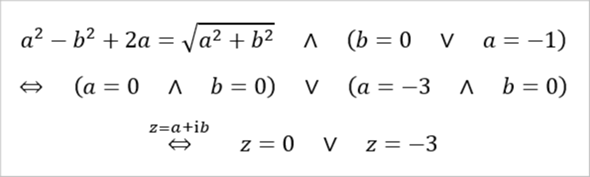
Ich danke dir vielmals! Hat mir sehr geholfen!
Ich habe gemerkt, dass ich einen Vorzeichenfehler gleich zu Beginn habe. Ich werde das gleich nochmal durchrechnen.
Ok vielen Dank für deine Mühen und deine Hilfe!
Ich habe das jetzt nochmal richtig durchgerechnet und komme auf 4 Lösungen. Nämlich...
z = 0
z = -3
z = 1 + i √((7 - √(17))/2) ≈ 1 + 1,1993i
z = 1 - i √((7 - √(17))/2) ≈ 1 - 1,1993i
Hier meine Rechnung dazu...
https://www.dropbox.com/s/dm4qifrdbn0djv3/KomplexeGleichung.pdf?dl=0
Zum Vergleich habe ich die Gleichung auch mal bei WolframAlpha eingegeben, wo man die gleichen Lösungen erhält, auf die ich auch gekommen bin.
https://www.wolframalpha.com/input/?i=solve%28z%5E2+%2B+2+*+conjugate%28z%29+-+abs%28conjugate%28z%29%29+%3D+0%29