Monotonie-Verhalten bei Funktionen ohne Nullstelle?
Es geht mir hierbei um die Aufgabe 5. Aufgabenteil a) und b) habe ich verstanden, allerdings verstehe ich c) und d) nicht ganz. Vor allem c) ist für mich kompliziert, da die Funktion keine Nullstelle hat. In den Lösungen wird jedoch gesagt, dass die Funktion streng monoton zunehmend ist. Kann jemand helfen?
Vielen dank!
1 Antwort
Wie kommst du darauf, dass c) keine Nullstelle hat?
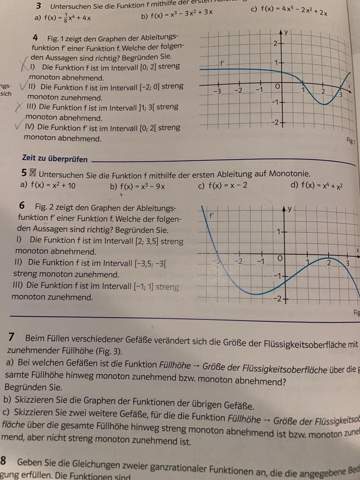
Die Funktion f(x)=x-2 ist eine lineare Funktion, folgt also dem Schema kx+d, und die Steigung ist 1, also positiv. Eine Nullstelle wäre bei x=2, weil 2-2=0.
Die erste Ableitung ist f'(x)=1, also auch positiv, deshalb ist das Monotonieverhalten streng monoton zunehmend.
Ich hab mich mit der Aussage auf die Ableitungsfunktion bezogen, nicht auf die normale Funktion. Danke!