Welchen Ansatz brauche ich für diese Aufgabe?
Hallo zusammen,
bei einer Probelektion bleibe ich gerade an einer Aufgabe hängen, eigens weiß ich nicht, wie ich anfangen soll/ wie ich rechnen muss und Google hilft mir da gerade auch nicht weiter.
Hoffe Ihr habt einen Ansatz oder könnt mir die Rechenwege gut/ausführlich erklären.
Danke für eure Mühe
Braunie
(Hoffe das Bild wird angezeigt. Aufgabe 10 a,b,c)
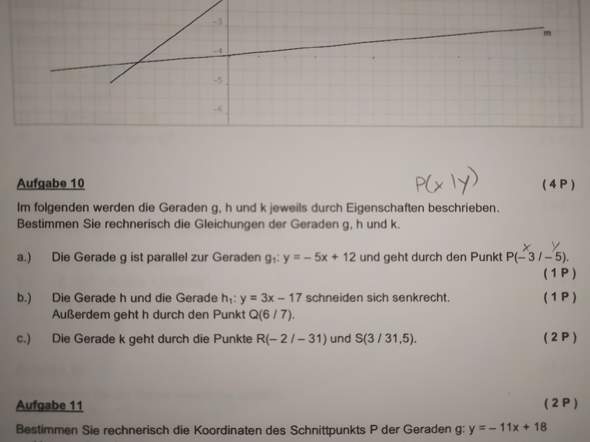
3 Antworten
10a) Alle Geraden von y = 5x + z laufen parallel. Das z kannst Du ausrechnen, wenn Du die Koordinaten aus Punkt P für x und y einsetzt.
10c) Geradengleichung aus 2 Punkten findest Du im Netz
https://www.frustfrei-lernen.de/mathematik/lineare-funktion-zwei-punkte.html
a)
weil parallel : m auch -5
-5 (die aus dem Punkt )
-5 = -5*-3 + b >>> b !
b)
weil senkrecht gilt für die beiden Steigungen
m1*m2 = -1
m2 daher -1/3
weiter wie a)
c)
m = (31.5 - - 31)/(3 - - 2)
einen der beiden Punkte nehmen und mit
-31 = m*-2 + b >>>> b !
b ) das ist ein Gesetz : stehen zwei Geraden senkrecht auf einander ist das Produkt der beiden Steigungen Minus 1 ....immer !
m1 = 2 ..... m2 = -1/2 ..............m1 = -0.3 .....m2 = +10/3
ob die Lösungen richtig sind , testet man selbst , indem man die Punkte einsetzt.
jede der drei gesuchten Geraden ist beschrieben durch f(x) = a*x + b
Du musst für jeden Fall a und b bestimmen. im ersten hast Du a gegeben (parallel, also gleiche Steigung und bestimmst b, indem Du "den Punkt in die Gleichung einsetzt (-5) = -5 * (-3) + b
im zweiten hat Du die Steigung durch "senkrecht" --> a= -1/3
Im Dritten zwei Gleichungen mit zwei ungekannten durch die beiden Punkte
Ersteinmal Danke für die schnelle Hilfe.
Ist bei a) die Lösung y=-5x+10
Und bei c) die Lösung y=0,5x-30
?:)
Nur b) verstehe ich leider noch immer nicht.
LG und vielen Dank nochmal