[Mathe] Hilfe - Funktionsterm mithilfe Abbildung aufstellen?
Guten Abend 😊
Hat jemand Lust, mir beim bestimmen der Funktionsterme bei dem Aufgabenteil a) zu helfen?
Wir müssen nur Lineare zweizeilige Gleichungssysteme lösen können.
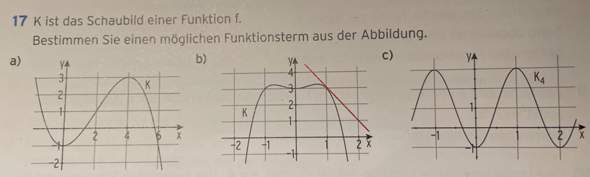
Bei a) habe ich es nicht hinbekommen, den Funktionsterm zu bestimmen.
Bei b) würde ich so vorgehen: Polynomfunktion 4. Grades, symmetrisch zur y-Achse -> nur gerade Exponenten im Ansatz. f(x) = ax^(4) + bx^(2) + c Und dann versuchen, es mit den gegebenen Bedingungen zu lösen.
Bei c) würde ich das Intervall ablesen, die Amplitude ablesen und die Höhe der Mittellinie und dann den Faktor k mithilfe der Periode berechnen.
5 Antworten
bei a) würde ich so vorgehen:
Ansatz: das ist ein Polynom 3. Grades, welches um 1 nach oben und 2 nach rechts verschoben ist.
Wenn der Wendepunkt im Ursprung liegen würde, wäre f(x) punktsymmetrisch und der Ansatz lautete:
f(x) = ax^3 + bx
f'(x) = 3ax^2 + b
f(2) = 2
f'(2) = 0
f'(2) = 0 = 3*a*4 + b
12a + b = 0 (1)
f(2) = 2 = a*8 + 2b
8a + 2b = 2 (2)
2*(1) - (2)
24a - 8a = -2
16a = -2
a = -1/8
b = 0 - 12a = 12/8 = 3/2
Damit:
f(x) = -1/8 x^3 + 3/2 x
Und nun verschieben wir das ganze um 1 nach oben und 2 nach rechts:
g(x) = -1/8 (x - 2)^3 + 3/2 (x - 2) + 1
Damit wäre die Aufgabe eigentlich schon gelöst. Man kann das aber auch verschönern...
und wir multiplizieren aus:
g(x) = -1/8(x-2)(x^2 - 4x + 4) + 3/2 x - 3 + 1
= -1/8(x^3 - 4x^2 + 4x - 2x^2 + 8x -8) + 3/2 x - 2
= -1/8 x^3 + 3/4 x^2 - 3/2 x + 1 + 3/2x - 2
g(x) = -1/8 x^3 + 3/4 x^2 - 1
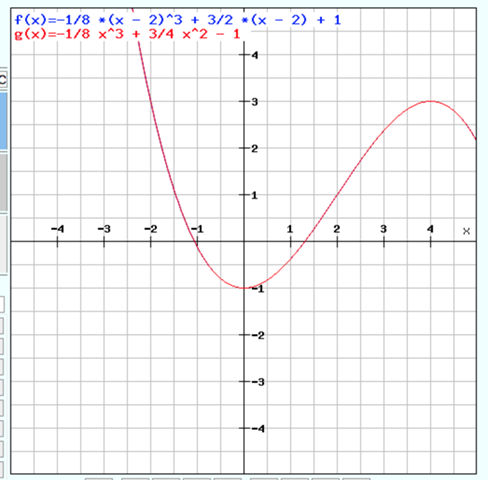
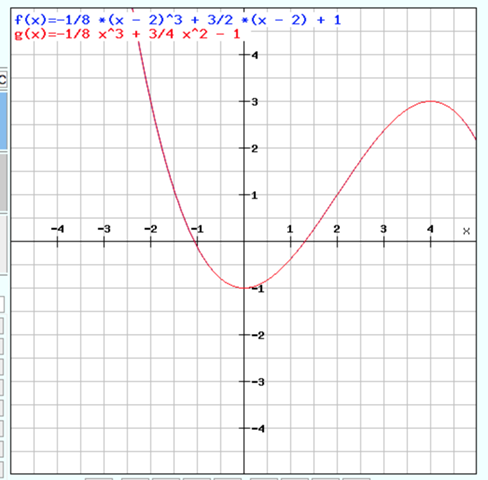
(kann das sein?).
möglich ist alles, würde mich aber wundern.
Das finde ich sehr kompliziert.
Die Geschmäcker sind verschieden. Ich find es einfacher.....aber es führen viele Wege nach Rom.
Geht das nicht mit den Bedingungen, die man sehen kann, ohne zu verschieben?
Das geht natürlich auch.
Für den allgemeinen Ansatz:
f(x) = ax^3 + bx^2 + cx + d
benötigt man dann halt 4 Bedingungen, zum Beispiel:
f(2) = 1
f ' '(2) = 0
f'(0) = -1
f'(4) = 3
Da wird dann halt das zu lösende Gleichungssystem etwas komplizierter (4 Zeilen)
Vielen Dank 💚 Ich gehe davon aus, dass in der Arbeit solche Aufgaben kommen werden bzw. eine und man nur das LGS aufstellen muss. Mehr muss man nicht machen, das steht dann so in der Aufgabe („Stelle ein LGS auf“).
Magst du dir noch meine Antwort auf die Hauptfrage hier ansehen? 😊
a) Du kannnst mit mit 3 Bedingungen nur 3 Parameter löösen, der 4. muss offen bleiben
f(x) = ax^(3) + bx^(2) + cx + d
f'(x) = 3ax^2 + 2bx + c
f(0) = 0 = a*0^(3) + b*0^(2) + c*0 + d
d = 0
f'(3) = 03a*3^2 + 2b*3 + c = 0
27a + 6b + c = 0
f(3) = 0 a*3^(3) + b*3^(2) + c*3 = 0
27a + 9b + 3c = 0
Wir haben also 2 Gleichungen:
27a + 6b + c = 0
27a + 9b + 3c = 0
und setzen diese gleich (andere Verfahren sind auch möglich):
27a + 6b + c = 27a + 9b + 3c
6b + c = 9b + 3c-2c = 3b
b = -2/3c
das setzen wir in die erste Gleichung ein:
27a + 6b + c = 0
27a + 6(-2/3c) + c = 0
27a - 4c + c = 0
27a = 3c
a = 1/9c
c können wir nicht lösen, also lautet die Funktion:
f(x) = 1/9 cx^3 -2/3 cx^2 + cx
Nun wählen wir 3 beliebige Zahlen für c:
1, -1, 9
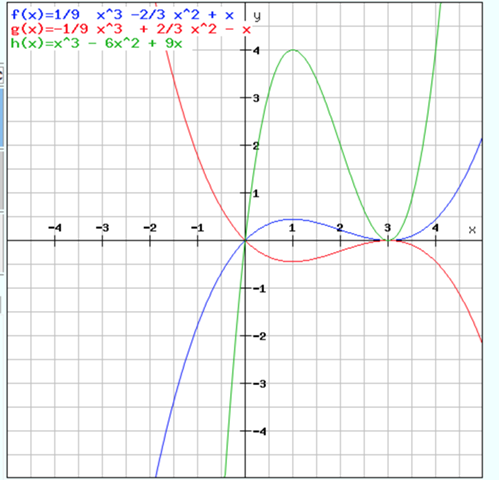
1) f(x) = 1/9 x^3 -2/3 x^2 + x
2) f(x) = -1/9 x^3 + 2/3 x^2 - x
3) f(x) = x^3 - 6x^2 + 9x
Das sieht dann so aus:
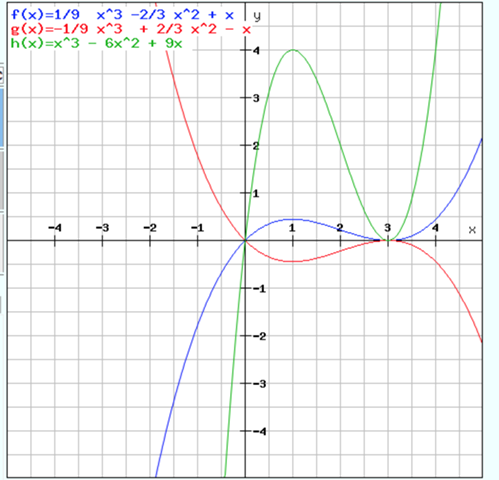
b) Jetzt haben wir eine 4. Bedingung und können auch c lösen:
Dazu machen wir die Punktprobe mit A(1 / 16/3 )
f(x) = 1/9 cx^3 -2/3 cx^2 + cx
f(1) = 1/9 c - 2/3 c + c = 16/3
mal 9:
c - 6c + 9c = 48
4c = 48
c = 12
und damit:
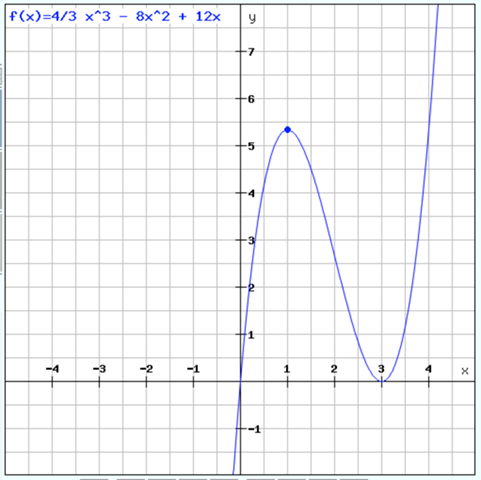
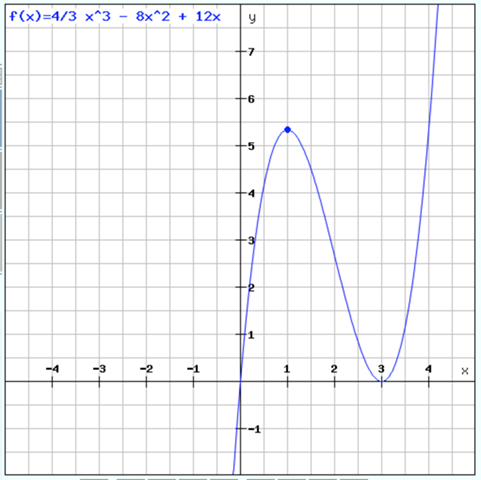
f(x) = 4/3 x^3 - 8x^2 + 12x
Hi Hamburger2, was ist das für ein Graphikprogramm - selber gemacht [Python] oder etwas Anderes. Danke!
Ich benutze je nach Bedarf zwei unterschiedliche Funktionenplotter:
https://rechneronline.de/funktionsgraphen/
Der erste ist etwas einfacher in der Bedienung und schöner in der Darstellung. Der zweite ist dafür viel flexibler und hat mehr Möglichkeiten zu besonderen Einstellungen.
Ist Mathematik Alpha eventuell bekannt; mein Tipp einfach mal reinschauen..
Wie weiß ich, welche Punkte in einer Funktion geändert werden können, sodass dennoch die Funktion die Bedingungen erfüllen, die in der Aufgabe stehen:
berührt die x-Achse in x = 3 und verläuft durch den Ursprung
Kann sich das nicht ändern, wenn ich einen beliebigen Wert einsetze?
Bei welchem Teil des Funktionsterms würde sich etwas ändern, wenn man wie hier du bei c einen beliebigen Wert eingesetzt hast?
Wie weiß ich, welche Punkte in einer Funktion geändert werden können, sodass dennoch die Funktion die Bedingungen erfüllen, die in der Aufgabe stehen:
Du hast ja in der Berechnung, bei der du die Anzahl von 4 Parametern auf einen reduziert hast, die entsprechenden Bedingungen berücksichtigt. Das Ergebnis nennnt man dann eine Funktionen- oder Kurvenschar, wobei alle diese Funktionen die gegebenen Bedingungen erfüllen, egal welchen Wert man für den freien Parameter einsetzt. Deshalb habe ich ja auch 3 beliebige Beispiele gewählt und die Graphen gepostet. Die Graphen sehen zwar unterschiedlich aus, aber die drei gegebenen Bedingungen erfüllen sie alle. Nur nebenbei: es ist völlig egal, ob ich die Gleichungen aus den Bedingungen nach a, b oder c auflöse und den Parameter dann in der Funktionsgleichung offen lasse.
Kann sich das nicht ändern, wenn ich einen beliebigen Wert einsetze?
Nein, denn die Bedingungen wurden in der Herleitung verarbeitet und deshalb erfüllen auch alle Funktionen diese, egal welchen Wert man für den freien Parameter wählt (außer 0 in der Regel, weil das dann kein Polynom mehr ist). Du kannst es ja selber mit einem Funktionenplotte ausprobieren. Egal, welchen Wert du für c wählst (außer 0), der entstehende Graph erfüllt die Bedingungen.
Bei welchem Teil des Funktionsterms würde sich etwas ändern, wenn man wie hier du bei c einen beliebigen Wert eingesetzt hast?
Da der freie Parameter, hier c, sich in allen Funktionstermen wiederfindet, ändern sich auch alle mit der Änderung von c. Entscheidend ist, dass die einzelnen Terme in einem bestimmten Verhältnis zueinander stehen, damit die Bedingungen erfüllt werden könnren. Diese erfoderlichen Verhältnisse der Parameter zueinander haben wir ja aus den Bedingungen und dem Lösen des LGS hergeleitet und in den allgemeinen Ansatz eingesetzt.
Vielen Dank für die ausführliche Antwort :-) Kannst du mir noch bei dieser Aufgabe weiterhelfen? 😬
(Seite 118 Nr. 17)
“K ist das Schaubild von f mit f(x) = 0,5e * e^(x); xeR. Zeigen Sie: K verläuft oberhalb der Geraden g mit der Gleichung y = e/2 (x + 1).“
Ansatz: Überprüfen, ob die beiden Funktionen Schnittpunkte haben. Wenn ja, verläuft K sowohl über als auch unter g. Wenn nein, an einem Beispiel prüfen, ob f(x) über oder unter g verläuft.
Schneiden beider Funktionen:
0,5e * e^x = e/2 (x + 1)
e^x = x + 1
Da wüsste ich keine analytische Lösung, sehe aber, dass x = 0 die Gleichung erfüllt.
e^0 = 0 + 1
1 = 1
Die haben also einen gemeinsamen Punkt. Das könnte auch ein Berührungspunkt sein. Das führt aber irgendwie zu nix.
Anderer Ansatz:
Wenn die Behauptung stimmt, muss gelten:
f(x) - g(x) > 0
0,5e * e^x - e/2 (x + 1) > 0
0,5e(e^x - x - 1) > 0
0,5e ist positiv. Also muss (e^x - x - 1) auch positiv sein.
Nun betrachten wir (e^x - x - 1) als eine Funktion und untersuchen sie auf Tiefpunkte, die immer oberhalb der x-Achse liegen müssen:
h(x) = e^x - x - 1
h'(x) = e^x - 1
h' '(x) = e^x
h'(x) = e^x - 1 = 0
e^x = 1
ln e^x = ln 1
x = ln1 = 0
Wir haben also nur ein Extremum bei x = 0.
h' '(0) = e^0 = 1 ...es handelt sich um einen Tiefpunkt.
h(0) = e^0 - 0 - 1 = 0
Ergebnis:
Für alle x ≠ 0 ist die Differenz von f(x) - g(x) positiv. Der Graph K verläuft daher über g. Nur für x = 0 ist die Differenz = 0. Da verläuft K nicht oberhalb von g, sondern die berühren sich.
Es ist unglaublich, das du das so viele Jahre nach der Schule noch alles kannst. Wirklich erstaunlich. Vielen vielen Dank für die Hilfe 💪
Das sind ja auch nur die ganz einfachen Sachen. Vieles kann ich auch nicht mehr. Speziell vieles aus dem Studium krieg ich gar nicht mehr hin.
Die einfachste Frage die es vermutlich gibt:
(Miniteil einer großen Aufgabe)
“Berechnung der Geraden, auf der die zwei Wendepunkte A(2/-5) und B(-2/-5) liegen.“
Meine Rechnung:
y = mx + b
m = (y2-y1)/(x2- x1) = 0
y = mx + b
y = b
Wie geht es weiter?
y(2) = 0*2 -5 = b
b = -5
Geradengleichung: y = -5
Dazu müsste man nicht einmal viel rechnen. Wenn sich der y-Wert bei verschiedenen x-Werten nicht ändert (siehe die Punkte), handelt es sich um eine Parallele zur x-Achse mit Abstand -5 und die hat die Gleichung:
y = -5
Morgen ist die Arbeit und ich rechne heute von jedem Thema Aufgaben, welche ich schon gelöst habe durch um die 1 zu holen morgen - hoffentlich. Dann hab ich die 1 als Anmeldenote für die Prüfung 💚💪
Ja das war logisch, hatte mich nur auf die x-Werte konzentriert, die y-Werte sind ja gleich.
Das heißt also, dass wenn die Steigung gleich 0 ist die y-Werte gleich sind und b = y ist. Wie konnte ich nicht darauf kommen 😅
Ich drücke dir die Daumen. Arbeite lieber konzentriert als hektisch....wegen der Leichtsinnsfehler. Und wenn am Ende Zeit übrig ist, mache so viel wie möglich Proben.
Ja, habe bei der letzten Arbeit sehr schnell gerechnet und versucht konzentriert zu sein. Habe dann am Ende noch so viel Zeit gehabt zum noch einmal ganz durchrechnen und hatte ein paar Fehler gefunden. Da hatte ich die 1,0 geschrieben. Vielen Dank 💚
Lehrer hat 30min vor der Klassenarbeit im Messenger geschrieben, dass er krank ist und wir sie nach den Ferien schreiben…
Eher nicht so gut. Schreibe nach den Ferien schon zwei arbeiten und jetzt drei und hatte die Nacht bis halb eins gelernt und mich gut vorbereitet gefühlt.
„K ist das Schaubild der Funktion f mit f(x) = a sin(bx); xeR. x = 3 ist eine Maximalstelle. K hat im Ursprung die Steigung pi/4. Bestimmen Sie einen Funktionsterm.“
Maximalstelle bedeutet soviel wie Hochpunkt und ich kann daraus also f‘(3) = 0 als Bedingung ziehen, richtig?
Wenn das so ist, dann ist die Aufgabe ganz einfach.
„Die Gesamtkosten in GE für die Herstellung einer Druckerpresse sind gegeben durch die Funktion K mit K(x) = 0,05x^(3) - 1,2x^(2) + 10x + 156; x >gleich 0. Zeigen Sie, mit zunehmender Produktionsmenge steigen auch die Gesamtkosten.“
Reicht es hier, einfach zwei x-Werte, z.B. x = 1 und x = 100 in die Funktion einzusetzen?
Oder versuche ich mögliche Hoch/-Tiefpunkte zu bestimmen durch f‘(x) = 0 setzen und dann einen Wert links daneben und einen rechts daneben in f‘(x) einsetzen, um die Monotonie zu bestimmen? Wenn kein Hoch-/Tiefpunkt vorhanden, einfach x = 0 in f‘(x) einsetzen.
Ja, ich glaube die erste Möglichkeit würde als Antwort nicht gelten, sondern nur die zweite. Hab’s mir glaube ich selber beantwortet.
Maximalstelle bedeutet soviel wie Hochpunkt und ich kann daraus also f‘(3) = 0 als Bedingung ziehen, richtig?
Würde ich auch so sehen.
Zeigen Sie, mit zunehmender Produktionsmenge steigen auch die Gesamtkosten.“
Genau, da ist zu zeigen, dass die Funktion für x > 0 streng monoton steigend ist. Die erste Ableitung ergibt eine quadratische Gleichung ohne Lösung für = 0 und hat damit keine Extrema.
f'(1) = 7,75, also positive Steigung und damit streng momnoton steigend.
Hey :-) Ich habe mal wieder eine kleine Frage 🙋♂️
(ein kleiner Aufgabenteil einer größeren Aufgabe)
f(x) = 1/4 e^(2x) -x + 2 mit dem Schaubild K.
“d) G ist eine Gerade mit h(x) = -x + 2. Begründen Sie, dass K stets oberhalb von G verläuft. Ermitteln Sie die Stelle, an der die Funktionswerte von f und h um 0,01 voneinander abweichen.“
Begründung:
K verläuft stets oberhalb von G, da K die Asymptote, die die Funktionsgleichung h(x) = -x + 2 hat, niemals berührt.
Wie kann ich die Stelle ermitteln, an der die Funktionswerte von f und h um 0,01 voneinander abweichen?
f(x) - h(x) = 0,01
1/4 e^(2x) -x + 2 - (-x+2) = 0,01
1/4 e^(2x) = 0,01
e^(2x) = 0,04
ln e^(2x) = ln 0,04
2x = ln 0,04
x = 1/2 ln 0,04 = -1,60944
Hinweis: beim Ziehen eines Logarithmus sollte man mit den Nachkommastellen nicht geizen, da sich Rundungsfehler im x-Wert nachher im Funktionswert exponentiell bemerkbar machen.
Probe:
f(-1,60944) = 1/4 * e^(-2*1,060944) +1,60944 + 2 = 3,61944
h(-1,60944) = +1,60944 + 2 = 3,60944
f(-1,60944) - h(-1,60944) = 3,61944 - 3,60944 = 0,01
Hast du noch Lust, mir bei einer weiteren Aufgabe zu helfen? :-)
“K ist das Schaubild der Funktion f mit f(x) = 1/3 x^(3) -x + 1; xeR.
a) Der Hochpunkt von K liegt in H(-1 | 5/3).
Geben Sie Tief- und Wendepunkt von K ohne weitere Rechnung an. Begründen Sie.
b) n ist die Normale von K im Wendepunkt.
Berechnen Sie die Koordinaten der Schnittpunkte von n und K.“
Wie ich vorgehen würde, ich denke, dass ich nur a) (den nicht rechnerischen Teil) nicht verstehe:
a) Verstehe ich nicht, wie ich das anhand der Funktion erkennen kann, da die Funktion f(x) ja sowohl gerade wie auch ungerade Potenzen enthält. Habe es auch schon in GeoGebra eingegeben, aber komme nicht auf den Grund.
b) Hier würde ich die Steigung der Wendetangente bestimmen und dann in die Funktion m1 * m2 = -1 einsetzen, um die Steigung der Normale zu bestimmen.
Dann noch eine Punktprobe, um den x-Achsenabschnitt b zu bestimmen. Dann die beiden Funktionen gleichsetzen, um ihre Schnittpunkte zu erhalten (nach x auflösen).
*um den y-Achsenabschnitt b zu bestimmen
a)
f(x) hat bezogen auf x nur ungerade Potenzen. Lediglich das +1 stört. Gäbe es kein +1, wäre die Funktion punktsymmetrisch zum Ursprung. Das +1 bedeutet, der Graph ist um 1 nach oben verschoben, sodass nun (0/1) zum Spiegelpunkt des Graphen wird.
Daher muss der x-Wert des Tiefpunktes bei x = +1 liegen, denn eine links-rechts-Verschiebung giobt es nicht. Nun muss der y-Wert von 5/3 am Punkt 1 gespiegelt werden. Differenz von 1 auf 5/3 = 2/3 nach oben. Um den Betrag gehts beim Tiefpunkt von 1 aus gesehen nach unten, also f(1) = 1 - 2/3 = 1/3. Damit erhalten wir: T(1/1/3).
b) Genau das ist der Lösungsweg.
Da muss rauskommen:
S1 = (0/1)
S2 = (√6 / 1+√6) = (2,45 / 3,45)
S3 = (-√6 / 1-√6) = (-2,45 / -1,45)
Großartige Antwort 💚
Letztes Jahr hatten wir in Mathe eine extrem hilfreiche Lehrerin. Sie hatte auf der Schulwebseite unter dem Fach Mathe eine Ablage gemacht, wo man Dateien hochladen konnte (Fotos von Mathe Aufgaben) und Fragen stellen konnte. Sie hat, wenn man um 20 Uhr eine Frage gestellt hat immer um ungefähr 01:00 Uhr nachts geantwortet. Mein jetziger Lehrer würde vielleicht nach 1-2 Tagen antworten und meine Deutsch Lehrerin z.B. antwortet nie auf eine Mail. Es gibt wirklich sehr große Unterschiede bei den Lehrern.
Und du bist meine größte Hilfe. Ohne dich hätte ich es bestimmt nicht geschafft, dieses Jahr auf einer 1 zu stehen. Du erklärst 100 mal besser wie die anderen hier auf Gutefrage.net. 💚 Oft sind es die kleinen Dinge an denen man hängt und man nur einen kleinen Tipp braucht.
Vielen Dank für die Hilfe 💚
Es gibt wirklich sehr große Unterschiede bei den Lehrern.
Das stimmt wohl. Da hatte ich in meiner Schulzeit das Glück, teilweise sogar ganz hervorragende Lehrer zu haben, speziell in Physik und Bio.
Du erklärst 100 mal besser wie die anderen hier auf Gutefrage.net.
Danke, das höre ich öfters.
Wohnst du in Süddeutschland? "besser wie" ist eigentlich der typisch schwäbische Komparativ.
Ja, in der Nähe von Stuttgart 😅
Aber ich rede/schreibe nicht wissentlich schwäbisch, ich mag schwäbisch sprechen nicht wirklich.
Erstaunlich, dass du das daraus ziehen konntest 😎
Na ja, als gebürtiger Schwabe, jetzt wieder wohnhaft ca. 70 km östlich von Stuttgart, und berufsmäßig mit Sprache und Schreiben beschäftigt, entwickelt man da eine gewisse Sensibilität.
Ich wohne 40km östlich von Stuttgart 😅😜
Bin auch hier geboren in Stuttgart.
Wir wohnen ja fast um die Ecke 😅
Wirklich cooler Zufall
Habe noch eine kleine Frage zu Mathe, die mich schon länger beschäftigt 🙋♂️💚 Zum Thema Wendestellen bestimmen (Notwendiges Kriterium/ Hinreichendes Kriterium)
Wenn ich eine Extremstelle bestimmen möchte, dann mache ich ja zuerst das Notwendige Kriterium (f‘(x) = 0 setzen) und dann das Hinreichende Kriterium (gefundene xe in f‘‘(x) einsetzen), um zu bestimmen, ob es sich um einen Hoch- oder Tiefpunkt handelt oder keine Aussage möglich ist, d.h. es einen Sattelpunkt gibt.
Das heißt also, dass es, wenn man nur das Notwendige Kriterium macht, es auch ein Sattelpunkt sein kann.
Bei der Berechnung der Monotonie ist es ja egal, ob es ein Sattelpunkt ist oder nicht, denn ich setze ja, nachdem ich die Stelle mit der Steigung = 0 gefunden habe (x-Wert), einen x-Wert links und einen rechts daneben in f‘(x) ein, um die Monotonie zu bestimmen.
Das bedeutet hier also, dass es entweder ein Hochpunkt, Tiefpunkt, oder ein Sattelpunkt geben kann.
__________-
Wenn ich eine Wendestelle bestimmen möchte, dann mache ich zuerst das Notwendige Kriterium (f‘‘(x) = 0 setzen) und dann das Hinreichende Kriterium (gefundene xw in f‘‘‘(x) einsetzen), um zu überprüfen, ob es ein links-rechts-Krümmungswechsel (Wert negativ) oder ein rechts-links-Krümmungswechsel (Wert positiv) ist.
Wenn hier bei der Hinteichenden Bedingung (gefundene xw in f‘‘‘(x) einsetzen) gleich Null rauskommt, um was handelt es sich dann?
Denn die hinreichende Bedingung brauche ich ja auch nicht unbedingt für die Untersuchung des Krümmungsverhaltens. Hier kann man ja einfach einen Wert links und einen Wert rechts neben der Wendestelle einen x-Wert in f‘‘(x) einsetzen, um die Krümmung zu bestimmen.
[Hat sich erledigt die Frage 😬 Jetzt sind bei mir wieder ein paar mehr Synapsen verknüpft! :-)]
Ahhh. Dann haben wir auch einen Sattelpunkt, wenn die gefundenen xw von der zweiten Ableitung nach dem gleich null setzen in die dritte Ableitung eingesetzt gleich Null ergeben. Ein Sattelpunkt mit waagrechter Tangente kann auch eine Wendestelle sein.
Hier spielt es also auch keine Rolle, ob man bei der Bestimmung des Krümmungsverhaltens das Hinreichende Kriterium macht, wenn man einen Wert links und rechts neben der Wendestelle in die zweite Ableitung einsetzt, um die Krümmung zu erhalten.
Ich habe es voll und ganz verstanden jetzt. Habe es nochmal auf meiner ausgedruckten Übersicht von dir angeschaut (habe es dort schonmal angeschaut aber irgendwie nicht im Zusammenhang verstanden). Wirklich unglaublich hilfreich!!!! Unglaublich… 💚
Es ist einfach nur eine Frage von Fleiß. Mein Mathe Lehrer sagte uns schon mehrmals „Wenn ihr in Mathe nicht so gut seid oder es nicht versteht, dann ist es auch nicht so schlimm. Schaut halt, dass ihr es schafft, durchzukommen.“ ≈ so ähnlich.
Kann das bis heute nicht verstehen. Er muss ja selber wissen, dass es fast immer nur eine Frage von lernen und Fleiß her ist, die Mathematik in der Schule zu verstehen. Und die meisten mit schlechten Noten sind einfach Faul oder konzentrieren sich zu wenig auf die Schule. 🤔
Aber was ist der Unterschied dann genau zwischen den beiden Sachen:
- Bestimmung der Extremstellen. Notwendiges Kriterium (f‘(x) = 0 setzen). Hinreichendes Kriterium (gefundene xe in f‘‘(x) einsetzen). Lösung = 0. Das bedeutet es ist ein Sattelpunkt
- Bestimmung der Wendestellen. Notwendiges Kriterium (f‘‘(x) = 0 setzen). Hinreichendes Kriterium (gefundene xw in f‘‘‘(x) einsetzen). Lösung = 0. Das bedeutet, es ist ein Sattelpunkt.
Was ist hier der Unterschied bei den beiden Sattelpunkten?
An einem Sattelpunkt ist ja immer die Steigung gleich Null oder? Und es ist doch auch immer die Krümmung gleich Null, richtig?
Ohhh habe ich hier gerade viel geschrieben. Ich wollte eigentlich gar keine Kurzgeschichte schreiben… ✍️ 😬😅 💚💚💚💚
Komme jetzt nicht ganz mit, was sich erledigt hat und was nicht. Greife daher mal einzelne Bemerkungen raus:
Ein Sattelpunkt mit waagrechter Tangente kann auch eine Wendestelle sein.
Das ist nicht ganz korrekt. Ein Sattelpunkt ist immer eine Wendestelle mit waagrechter Tangente. So ist er definiert. Das "kann" muss durch ein "muss" ersetzt werden. Definition: "Eine Wendestelle mit waagrechter Tangente wird Sattelpunkt genannt." Daher hat ein Sattelpunkt zwei notwendige Bedingungen: waagrechte Tangente (f ' = 0) und Wendepunkt (f ' ' = 0) sowie für den Wendepunkt die hinreichende Bedingung f ' ' ' ≠ 0.
Kann das bis heute nicht verstehen. Er muss ja selber wissen, dass es fast immer nur eine Frage von lernen und Fleiß her ist, die Mathematik in der Schule zu verstehen. Und die meisten mit schlechten Noten sind einfach Faul oder konzentrieren sich zu wenig auf die Schule.
Da möchte ich dich vor voreiligen Schlüssen und der Gefahr der Arroganz warnen. Das obige kann ein Grund sein muss es aber nicht sein (schlechte Noten sind keine keine hinreichende Bedingungen, um auf Faulheit schließen zu können.). Die Talente sind nun mal verschieden verteilt. Um sehr gut in Mathe zu sein, gehört Fleiß dazu (notwendige Bedingung) reicht aber eventuell nicht aus. Es gibt auch Leute, denen fehlt die Fähigkeit zum abstrakten Denken und die können sich anstrengen, wie sie wollen, ohne auf einen grünen Zweig zu kommen. Habe selber schon Leute inmeinem Berufsleben erlebt,deren abstrakte Inteligenz ging gegen 0, dafür hatten die aber eine enorme praktische Intelligenz. Die haben bei defekten Maschinen nur hingeguckt, wo was kapuut war und haben praktisch alles irgendwie repariert oder durch Improvisation wieder zum Laufen gekriegt. Auch die braucht man. Dafür gibts Mathegenies, die scheitern daran, den Fotokopierer richtig zu bedienen oder Öl im Motor nachzufüllen.
Bestimmung der Extremstellen. Notwendiges Kriterium (f‘(x) = 0 setzen). Hinreichendes Kriterium (gefundene xe in f‘‘(x) einsetzen). Lösung = 0. Das bedeutet es ist ein Sattelpunkt
Das ist nicht ganz korrekt. Das wären die beiden notwendigen Kriterien für einen Sattelpunkt. Zusätzlich muss eine der beiden hinreichenden Bedingungen für eine Wendestellle erfüllt sein: entweder f ' ' ' ≠ 0 oder erfülltes Vorzeichenwechselkriterium für f ' '.
Habe übrigens nochmal die Zusammenfassung ergänzt. Man beachte Kap. 12. Vielleicht wird das dann klarer und gibt einen Handlungsfaden, wie man bei Extremstellen der Reihe nach vorgeht:
Die Talente sind nun mal verschieden verteilt. Um sehr gut in Mathe zu sein, gehört Fleiß dazu (notwendige Bedingung) reicht aber eventuell nicht aus. Es gibt auch Leute, denen fehlt die Fähigkeit zum abstrakten Denken und die können sich anstrengen, wie sie wollen, ohne auf einen grünen Zweig zu kommen.
Stimmt, das hast du eindeutig besser gesagt. 👍 Bei vielen ist die notwendige Bedingung (lernen) nicht vorhanden, bei anderen schon und manche davon können es trotzdem nicht verstehen.
Danke für deine Ergänzung. :-) Magst du sie mir vielleicht nochmal erklären? 🤔
Komme da ein bisschen durcheinander, was wo eingesetzt wird bzw. was gleich 0 gesetzt wird (bei der Abbildung; bei Aufgaben verstehe ich es ja) sehe ich hier nicht so ganz 😬
Echt großartig, dass du die Übersicht anpassen tust und du dir die Mühe machst 😊💚
Das Schaubild in Worten:
Das Schaubild stelt die sinnvolle Reihenfolge dar, wie man die besonderen Stellen effizient ermittelt:
1) f' = 0 setzen und damit die Punkte mit waagrechter Tangente suchen. Diese Punkte habe ich mit x1 bezeichnet, kann aber auch mit x2, x3 etc bis xn weitergehen. Es gilt dann immer entsprechendes.
2) Dann x1 ... xn in f ' ' einsetzen. Für f ' ' < 0 hat man einen Hochpunkt und kann aufhören. Für f ' ' > 0 hat man einen Tiefpunkt und kann aufhören.
2a) Falls man Wendepunkte sucht, steigt man bei f ' ' = 0 ind das Schaubildein.
2b) Falls f ' ' = 0, gehts mit dem roten Pfeil weiter.
3) x1 ...xn in f ' ' ' einsetzen. für f ' ' ' ≠ 0 kann man aufhören und man hat einen Wendepunkt. Wenn f' an der Stelle ≠ 0 ist, hat man einen normalen Wendepunkt. Wenn f' = 0 ist, hatman einen Wendepunkt mit waagrechter Tangente, also einen Sattelpunkt.
4) Falls f ' ' ' = 0 ist, ist noch nicht klar, ob man an x1...xn eine Extremstelle hat. Dann muss man mit dem Vorzeichenwechselkriterium VWK weitermachen.
5) Kann man für f' ± x einen Vorzeichenwechsel (VW) feststellen, hat man einen HP oder TP und kann aufhören.
6) Hat man für f' ± x keinen Vorzeichenwechsel, muss man den VW für f ' ' ± x überprüfen. Hat man einen VW, hat man einen WP und kann aufhören. Hat man keinen VW, gibts hier für x1 ... xn keine besondere Stelle.
Wenn man nach dem Schema systematisch vorgeht, hat man mit Sicherheit umd effizient alle besonderen Punkte erfasst und ermittelt.
Vielen Dank für die viele Mühe 💚 Das mit Vorzeichenwechselkriterium hatten wir noch nicht, vielleicht kommt das ja noch.
Oder das fällt untern Tisch. Wenn das eine normale Klausur/Prüfung ist, muss auch nicht unbedingt mit Sattelpunkten und erforderlichen Vorzeichenwechselkriterien gerechnet werden. Dann kommt man ohne diese Spezialitäten glatt durch. Da muss man dann nur Flüchtigkeitsfehler vermeiden und ganz besonders immer auf die korrekten Vorzeichen achten.
Beim lesen deiner Antwort sieht es logisch aus 😅 Werde es dann nochmal selbst versuchen 💚 Unendlich danke 🙏 Du kannst so wunderbar erklären.
zu a)
f(x) = a * x³ + b * x² + c * x + d
Bedingungen:
f(0) = -1
f'(0) = 0
f(4) = 3
f'(4) = 0
zu b)
Funktion passt
Bedingungen:
f(0) = 3
f(1) = 3
f'(1) = -2
Hier brauche ich noch etwas Hilfe bei der Aufgabe 5 und 6 🙋♂️😊
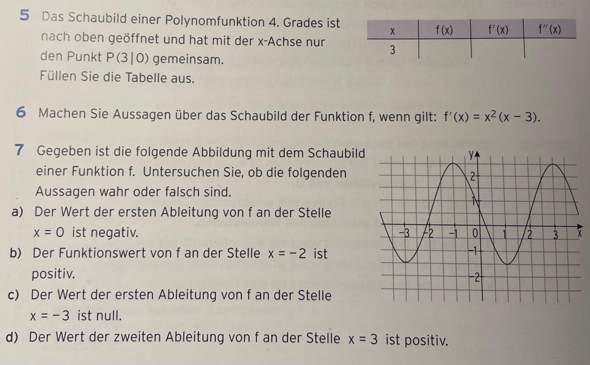
Aufgabe 7 habe ich denke ich mal richtig gelöst.
Bei Aufgabe 5 weiß ich nicht, wie genau ich die Tabelle ausfüllen muss. Ich weiß nicht, wie man das macht, dass eine Polynomfunktion 4. Grades nur einen Punkt mit der x-Achse hat. Man hat ja auch nicht genügend Bedingungen, um die Funktion aufzustellen, also in meinen Augen jedenfalls.
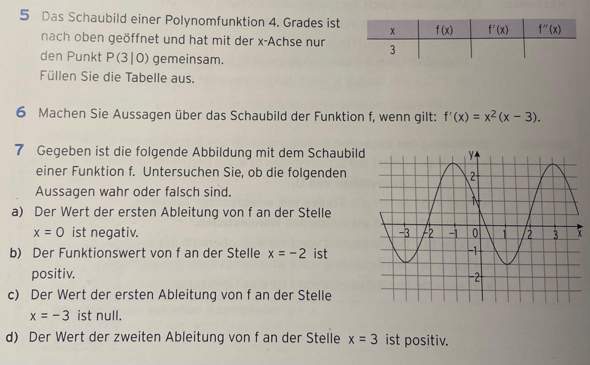
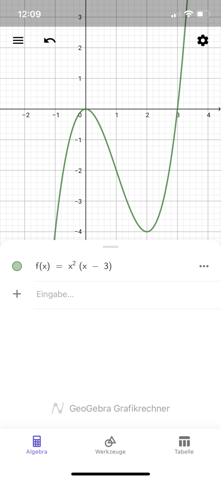
Bei Aufgabe 6 bekomme ich auch noch nicht hin. Hier ist ja der Nullstellenansatz. Aber dieser zeigt ja nur in der normalen Funktion die Nullstellen und nicht in der ersten Ableitung (oder?). Ist bei x = 0 ein Sattelpunkt (doppelte Nullstelle bei der Ableitung)? Und wie könnte man das begründen, dass das ein Sattelpunkt ist? Und bei x = 3 ist die Steigung Null.
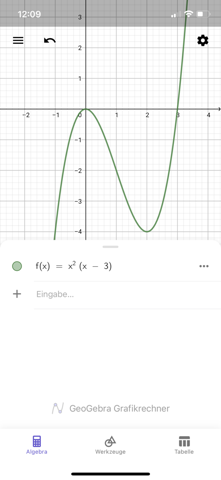
Bei Aufgabe 7 würde ich folgendes behaupten:
a) Dies ist wahr, da hier die Steigung negativ ist.
b) Dies ist wahr, da der y-Wert an der Stelle x = -2 positiv ist.
c) Dies ist wahr, da die Steigung an der Stelle x = -3 gleich Null ist.
d) Dies ist falsch, da die Krümmung weder positiv noch negativ ist. Die Krümmung ist gleich Null, da sich hier ein Wendepunkt befindet.
Das sind offensichtlich Aufgaben, wo man nicht rechnen muss, sondern wo es um qualittaive Aussagen geht.
Aufgabe 5:
Wenn der Graph nach oben offen ist, dann kann der einzige Punkt mit der x-Achse nur der tiefste Tiefpunkt (= globales Minimum) sein. Läge der tiefste Tiefpunkt oberhalb der x-Achse, gäbe es gar keinen Schnittpunkt mit der x-Achse, läge er drunter, müsste es mindestens zwei Nullstellen geben.
Wenn P(3/0) ein Tiefpunkt ist, kann man sagen:
f(3) = 0; f'(3) = 0; f ' '(3) > 0
Aufgabe 6)
Das hast du eigentlich schon ziemlich gut analysiert. Da ist mal wieder unser heiß geliebter Sattelpunkt. Wenn die erste Ableitung eine doppelte Nullstelle bei x = 0 hat, hat die zweite Ableutung mindestens noch eine an der Stelle: also Wendepunkt mit waagrechter Tangente: Sattelpunkt im Ursprung.
Die zweite Nullstelle bei x = 3 lässt den sicheren Schluss zu, dass es sich um eine Extremstelle, also Hoch- oder Tiefpunkt handelt. Um was es sich handelt, haben wir schnell rausgekriegt:
f'(x) = x^2(x -3) = x^3 - 3x^2
f ' '(x) = 3x^2 - 6x
f ' '(3) = 27 - 18 = 9
> 0, also Tiefpunkt
Weitere mögliche Aussagen: Die Funktion ist 4. Grades und nach oben offen, das x^3 integriert 1/3 x^4 und damit der Parameter a positiv ist.
Da alle Nullstellen von f' erledigt sind, gibt es keine weiteren Extremstellen auper dem Tiefpunkt.
Aus
f ' '(x) = 3x^2 - 6x = x(3x - 6) folgt für weiter Wendestellen:
3x - 6 = 0
x = 2
Es gibt eine weitere Wendestelle bei x = 2
Da es nur einen Tiefpunkt gibt folgt:
Die Funktion ist im Intervall (-∞; 3] monoton fallend
und im Intervall (3; ∞) streng monoton steigend
7)
d) ist falsch beantwortet.
Korrekt: Antwort ist falsch. Bei x = 3 befindet sich ein Hochpunkt, also muss die zweite Ableitung negativ sein.
Lese es gerade nochmal durch....da sind ja Rechtschreibfehler ohne Ende drin. Wenn du welche findest, darfst du die gerne behalten.
Es ist echt mies wenn man Corona bekommen sollte. Ich lerne so viel, stehe auf einer 1,5 im Durchschnitt und würde ich durch Corona fehlen, dann würde ich mal eben 3 arbeiten und viel Unterrichtsstoff verpassen.
Gestern hatte jemand aus meiner Familie einen direkten Corona Kontakt mal wieder.
Ich bete dass ich gesund bleibe… und ein geilen Abschluss schaffe…
Die behalte ich immer ;-) Deinen Inhalt versteht man ja immer und er ist immer super hilfreich.
Könnte ich bei Aufgabe 6 auch einfach die normale Funktion bestimmen durch aufleiten?
Und dann Extremstellen, Wendestellen, Krümmungsverhalten und Monotonie bestimmen?
In der Aufgabe ist nicht genau ersichtlich, was genau gefordert wird.
Heißt „Machen Sie Aussagen“ nicht, dass man nichts rechnen muss?
Könnte ich bei Aufgabe 6 auch einfach die normale Funktion bestimmen durch aufleiten?
Das wäre auch eine Möglichkeit. Könnte mir aber vorstellen, dass das im Verhältnis zur erreichbaren Punktzahl zu viel Zeit kosten könnte und dann womöglich doch nicht das ist, was erwartet wird, also rein qualitativ erkennen zu können, was sich hinter einer Gleichung versteckt.
In der Aufgabe ist nicht genau ersichtlich, was genau gefordert wird.
Genau das ist das Problem.
Heißt „Machen Sie Aussagen“ nicht, dass man nichts rechnen muss?
Da sind auf jeden Fall Worte und nicht Zahlen gefragt.
Ich verstehe folgende Aufgabe nicht und habe noch ein paar Fragen zu der Aufgabe:
“Der Graph einer Polynomfunktion f 3, Grades berührt die x-Achse in x = 3 und verläuft durch den Ursprung.
a) Geben Sie für drei verschiedene Funktionen, die die gegebenen Bedingungen erfüllen, den Funktionsterm an.
b) Weiterhin liegt der Punkt A(1/ 16/3 ) auf dem Schaubild der Funktion. Bestimmen Sie den Funktionsterm dieser Funktion.“
Vorgehensweise bei a):
Ich würde die Funktion dritten Grades aufschrieben.
f(x) = ax^(3) + bx^(2) + cx + d
Mein wissen ist nur, dass ich nur zweiteilige LGS können muss.
Ich habe hier glaube ich nur 3 Bedingungen:
f(0) = 0
f(-3) = 0
f‘(-3) = 0
Ich weiß nicht, wie ich das machen kann. Könnte man eine Funktion dritten Grades einfach ändern, z.B. so:
f(x) = ax^(3) + bx + c
oder
f(x) = ax^(3) + c
Ich habe keine Ahnung…
Nach rechts verschieben kenne ich nicht. Ich glaube, dass wir das nicht haben (kann das sein?).
Das finde ich sehr kompliziert. Geht das nicht mit den Bedingungen, die man sehen kann, ohne zu verschieben? 🤔😬