Lyapunov Funktion - Stabilität bestimmen?
Das hier ist die Aufgabe. Ich soll herausfinden ob V eine Lyapunov-Funktion ist und die Stabilität bestimmen:

Mein bisheriger Rechenweg sieht so aus:
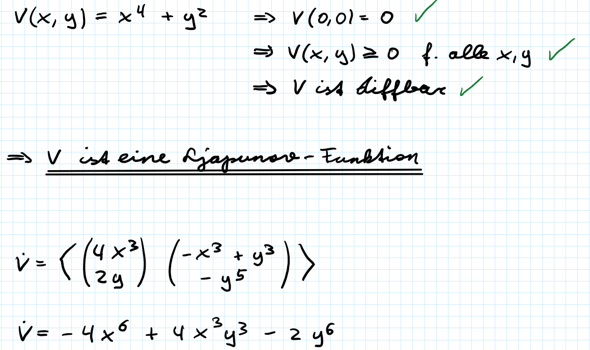
Nun hab ich das Problem, dass ich einen Term dritter Potenz habe, bei dem sich das Vorzeichen ändern kann und ich somit keine Aussage treffen kann. Der Versuch ein zusätzliches Störpolynom an V anzuhängen (hatte es mit Ax^2 + Bxy + Cy^2 und mit Ax^3 + Bx^2y + Cxy^2 + Dy^3 versucht), hat bisher nicht geklappt. Jemand eine Idee?
2 Antworten
Zerleg den Term mal so, dass eine binomische Formel passt.
Vorfaktor -2 und Variablen x³ und y³ bieten sich an.
Dann nutze, dass das Quadrat einer reellen Zahl immer nichtnegativ ist.
Sicher doch.
(Übrigens hatte ich an -2 (x³+y³)² gedacht, aber das ist letztlich dasselbe, nur etwas einfacher ausgedrückt.)
Alles klar danke :)
Aber sicher, dass das der richtige Ausdruck wäre? denn dann wäre mein zweiter Eintrag ja negativ und ich benötige hier ja einen positiven.
Also im Endeffekt
-2 (x³+y³)² = -2x^6 - 4x^3y^3 - 2y^6 != -4x^6 + 4x^3y^3 - 2y^6
Oder hab ich da was vercheckt :D
Stimmt, da hab ich nicht genau hingeschaut, sorry.
Zweite binomische Formel:
-2 (x³ - y³)²
(anderes Rechenzeichen in der Klammer)
Beachte : (x^3 - y^3)^2 = x^6 - 2x^3y^3 + y^6
--> dV/dt = (-2)*(x^3 - y^3)^2 - 2*x^6 < 0
für alle (x, y) aus IR^2\{0}.
Also im Endeffekt:
-1/2 * (2x^3 - 2y^3)^2 - 2x^6
Der Ausdruck ist also asymptotisch stabil, da der Ausdruck in Summe negativ ist oder?