lokale änderungsrate zu 1-x²
momentane änderungsrate f(x)= 1-x², x0= 1 also ich habe das so gerechnet: f(x)-f(1) / x-1 = 1-x² -0 /x-1 = (1-x) (1+x) / x-1 so und da hänge ich , weil ich da ja nichts wegkürzen kann, das ergebnis muss -2 sein. bitte kann mir jemand zeigen wie das weitergeht und bitte ohne h formel, weil die haben wir nicht gemacht. ich weiss dass man das auch über differentialrechnung machen kann, das haben wir aber noch nicht, wir benutzen die formel f'(x)= lim x-->x0 f(x)-f(x0)/x-x0
2 Antworten
(1-x² -0)/(x-1) = -(x²-1)/(x-1) = -(x+1)(x-1)/(x-1) = -(x+1)
Das geht gegen -2 für x gegen 1.
Das ist ja nicht "einfach umgedreht", d.h. es wurden nicht einfach die beiden Summanden vertauscht, sondern es wurde erst mal der Faktor -1 ausgeklammert. Und ob ich dann in der Klammer -1+x² oder x²-1 schreibe, das ist dann nach Kommutativgesetz tatsächlich dasselbe.
Hey,
hier gibt es gleich drei Methoden (wobei sich die dritte aus der zweiten ableitet):
a) Ableitung
b) lokale Änderungsrate
c) h-Methode
Also haben wir:
a) f(x) = -x² +1 (habe nur die Summanden vertauscht)
x0 = 1
f'(x) = -2x
Also haben wir:
f'(x0) = f'(1) = -2*1 = -2
Die Steigung ist also -2.
b) lokale Änderungsrate:
f'(x0) = lim (x → x0) f(x)-f(x0) / x-x0
Das ist deine Formel. Nun setzt du ein:
lim (x→ x0) (1-x²-0)/(x-1)
Nun kannst du den Term im Zähler umformen. Und zwar lautet der Term
1-x²,
das ist eine ausmultiplizierte binomische Formel. Und zwar die dritte, die allgemein lautet
(a+b)(a-b) = a² - b²
Wir wenden sie nun rückwärts an:
1-x² = (1+x)(1-x)
Wir setzen ein:
lim (x→ x0) ((1+x)(1-x))/(x-1
Nun wollen wir ja kürzen! Dazu klammern wir zuächst im Zähler -1 aus. Der Term lautet
(1-x)(1-x),
-1 ausgeklammert ergibt im Produkt
-1+x², also x² -1,
was wieder als dritte Binomische Formel
(x+1)(x-1)
ist. Wir ersetzen nun; das - natürlich nicht vergessen!
lim (x→ x0) (-(x+1)(x-1))/(x-1)
Nun kannst du x-1 kürzen, da wir im Zähler ein Produkt haben:
lim (x→ x0) -(x+1)
Jetzt setzen wir x = x0, da wir keinen Bruch mehr haben und somit der Nenner nicht Null werden kann:
f'(x0) = -2
c) h-Methode:
Diese ergibt sich aus der zweiten. Der Term x-x0 wird einfach durch h ersetzt, wobei der Limes von h ganz offensichtlich gegen Null laufen muss. Wenn x gegen x0 löuft, wird die Differenz immer kleiner, bis sie letztlich Null ist. Unser h gibt ja die Differenz an, weshalb h gegen Null laufen muss:
h = x-x0
Nun nach x umstellen:
x = x0+h.
Wir ersetzen also in der Formel der lokalen Änderungsrate unsere Terme und erhalten
f'(x) = lim (h → 0) f(x0+h)-f(x0)/h
Damit arbeiten wir jetzt:
lim (h→0) 1-(1+h)² -0 / h
Nun die binomische Formel auflösen:
(1+h)² = 1 +2h +h², oder anders geschrieben h² +2h +1.
Wir können nun diesen Term einsetzen:
lim (h→0) (1-(h²+2h+1))/h
Nun vereinfachen wir:
lim (h→0) (-h² -2h)/h
Schau, wir haben im Zähler zwei Terme mit h. Laut dem Distributivgesetz können wir jetzt ein h ausklammern:
lim (h→0) h(-h-2)/h
Nun können wir kürzen:
lim (h→0) -h-2
Nun setzen wir h = 0,da unser Bruch wen ist:
f'(x0) = -2
Du siehst: Egal, welchen Weg ich gehe, unser Ergebnis ist immer -2. Diese lokale Änderungsrate ist auch die Steigung deiner Funktion f am Punkt P(1|0). Das sind Methoden, mit denen du das bestimmen kannst. Die erste Methode leitet sich eigentlich aus der dritten her - siehe Anhang :)
Hoffentlich konnte ich dir helfen :)
Bei Fragen melde dich!
LG ShD
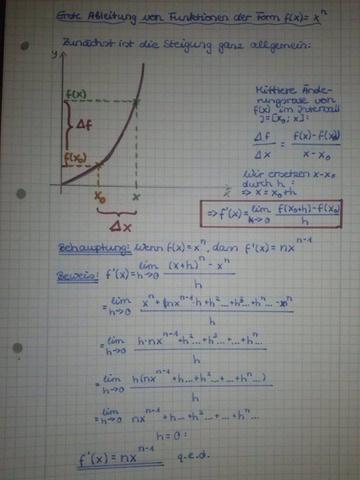
ja so hatte ich mir das auch gedacht.
aber geht das denn dass du einfach 1-x² umdrehst zu x²-1 im zweiten schritt. das war nämlich genau mein problem