Kann man einen 35 grad Winkel konstruieren oder muss man das geodreieck benutzen?
Ich glaube man könnte ein 75 grad Winkel konstruieren und dann eine Winkelhalbierende .. Oder? Wie geht das
5 Antworten
Du musst einen Stich machen->eine Gerade. Dann legst du das Geodreieck mit der null an einem Ende der Linie an und misst dann außen an diesem Bogen 35 Grad ,da machst du dann einen kleinen Punkt den du dann mit dem Ende der Linke verbindest.

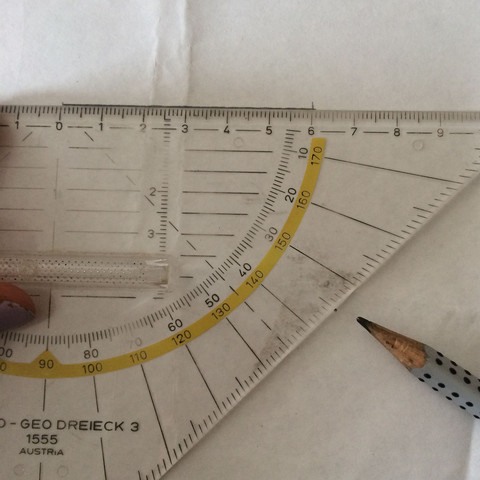
Und einen 35 Gradwinkel zu konstruieren ist allein Zirkel und Lineal leider nicht möglich ohne konkrete Winkel auszumessen. Damit meine ich, dass der Winkel nicht einfach abgetragen wird, weil dann ginge es. Denk dir also einfach den Winkelmesser von deinem Geodreieck weg. Das einzusehen ist relativ schwierig, da brauchst du das Wissen über Körpertheorie. Das rein geometrisch zu begründen ist nicht oder sehr schwer möglich.
Gruß
Zuerst konstruiert man nen Winkel von 90 Grad und dann drittelt man ihn. Das ist im Allgemeinen möglich.
Nein, konstruktive Drittelung eines Winkels ist "im Allgemeinen" eben nicht möglich - das wurde vor gut 180 Jahren von Pierre-Laurent Wantzel bewiesen.
Es geht nur in speziellen Fällen, der 90°-Winkel gehört dazu - aber im Grunde drittelt man den rechten Winkel dann gar nicht, sondern konstruiert zwei 60°-Winkel hinein
Die Winkelhalbierende eines 75° Winkels ergibt zwei Winkel von jeweils 37,5°. Dann hast du aber immer noch keinen 35° Winkel. Wenn Du in der Lage bist einen 75° Winkl zu konstruieren, dann mach es doch genauso mit dem 35° Winkel. Soweit ich weiß, geht das ohne Winkelmesser nicht.... :-(
75° lässt sich konstruieren, weil 75° = 60° + 15°, und weil man den 60°-Winkel über ein gleichseitiges Dreieck und den 15°-Winkel aus zweifacher Halbierung von 60° konstruieren kann. (Oder einfacher 75° = 30° + 45°, 30° und 45° sind halbierte 60° bzw. 90°)
Konstruieren lassen sich meines Wissens nur
- 90° und 60°,
- alle Winkel, die sich aus fortgesetzter Halbierung von 90° oder 60° ergeben (also 45°, 22,5°, 11,25°, ... , 30°, 15°, 7,5°, 3,75°, ...) sowie
- alle Summen aus den zuvor genannten Winkeln (wobei man damit die direkte Konstruktion von 90° nicht braucht, denn 90 = 60 + 30).
35° passen da leider nicht rein ...
Upps - stimmt nicht ...
Natürlich lassen sich neben 90° und 60° auch die Innen- und Außenwinkel aller konstruierbaren regelmäßigen Polygone konstruieren. Die Sache mit dem fortgesetzten Halbieren und dem Summieren funktioniert damit natürlich auch.
Als Ergebnis lassen sich damit alle ganzzahligen Winkel konstruieren, die durch 3 teilbar sind (also 3°, 6°, 9°, ...), sowie deren fortgesetzten Halbierungen, die dann aber eben nicht mehr ganzzahlig sind.
35° geht trotzdem nicht, nur 36° oder 34,5° ...
http://www.mathelounge.de/103974/grad-winkel-konstruieren-lineal-zirkel-kein-winkel-abtragen
http://www.helpster.de/winkel-konstruieren-mit-dem-zirkel-so-funktioniert-s_97878
Zuerst 280 Grad winkel konstruieren (3 viertel von einem Kreis) und dann so viele male den Winkel halbieren bis du 35 hast
Die Hälfte von 75 ist nicht 35.
Zuerst konstruiert man nen Winkel von 90 Grad und dann drittelt man ihn. Das ist im Allgemeinen möglich. Dann hat man einen 30 Grad Winkel. Einen 45 Gradwinkel bekommt man über die WInkelhalbierende. Diese beiden Winkel fügst du dann zusammen und hast den 75 Gradwinkel.