Ist der Satz von Heron auf nichtrechtwinklige Dreiecke anwendbar?
Wenn nicht, wie kann ich den Flächeninhalt halt eines nichtrechtwinkligen Dreiecks, wo ich alle Seitenlängen habe ausrechnen?
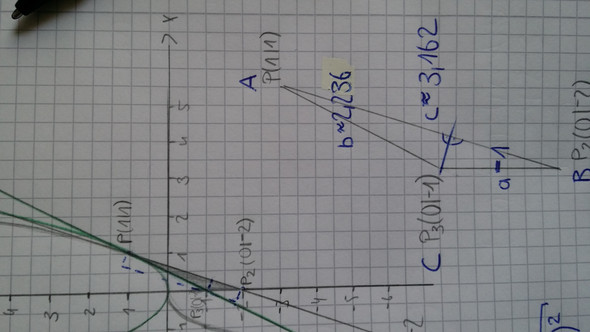
Die Höhe ist nicht gegeben
6 Antworten
Da könntest du auch zum Kosinussatz greifen und damit die Winkel des Dreiecks berechnen. Mit den Winkeln kannst du dann auf eine Höhe schließen und damit den Flächeninhalt des Dreiecks berechnen.
In jedem Dreieck gilt:
c² = a² + b² - 2ab * cos γ
b² = a² + c² - 2ac * cos β
a² = b² + c² - 2bc * cos α
Da du alle drei Seitenlängen a, b und c gegeben hast, kannst du die Formeln nach dem Winkel auflösen und diesen berechnen.
Dann lässt sich mit einfacher Trigonometrie im rechtwinkligen Dreieck die Höhe berechnen.
Aber auch der Satz von Heron ginge hier natürlich, je nachdem, was dir lieber ist.
LG Willibergi
Heron halte ich für Kürzer. Kannste zu.B. auf dem TR programmieren, den ersten Teil, wie man s findet, spar ich mir hier
Recall s ; Recall a ; Minus ; Recall s ; Recall b ; Minus ; Mal ; Recall s ; Recall c ; Minus ; Mal ; Recall s ; Mal ; Wurzel
Ist das für irgendeinen "vorsintflutlichen" HP- Rechner (gemahnt mich wirklich an die guten alten Zeiten) ?
Im vorliegenden Beispiel kommt man aber wirklich ohne Rechner aus, wenn man z.B. nur weiß, dass 1 * 1 = 1 und 1 : 2 = 1/2 .
(und wenn man eben hinschaut ...)
Der Satz von Heron gilt für das allgemeine Dreieck.
Du kannst ihn also auf jedes Dreieck anwenden - wie den Kosinussatz.
Rechnerisch ist Heron aber viel leichter zu behandeln als der Satz der Trigonometrie, eine Addition und eine Wurzel.
Wenn man's dann aber recht bedenkt, braucht man für die Spatzen am Ende doch zumindest ein Gewehr, dieweil die Höhe nur mit einem Kraftakt zu bestimmen ist, - und zwar mit der Verlängerung einer Seite. Das geht auch, weil die x-Koordinaten zweier Punkte identisch sind. Da muss man aber erst mal drauf kommen. Außenliegende Höhen sind nicht die größten Freunde der Schüler.
Guter Einfall!
Für das vorliegende Dreieck geht es ganz einfach, ohne Brimborium und Heron und Cosinussatz !
Beachte einfach, dass man die Längen der Seite a und der zugehörigen Höhe ha sofort aus den gegebenen Koordinaten der Eckpunkte des Dreiecks ablesen kann !
Ja, der Satz von Heron gilt für alle Dreiecke.
LG Leon
Die Länge der Seite AB stimmt offenbar. Du musst aber noch die Längen der anderen beiden Seiten berechnen.