Flächeninhalt gleichschenkliges Dreieck?

Gibt es eine Möglichkeit, den Flächeninhalt eines gleichschenkligen Dreiecks nur mithilfe einer Höhe und einem Winkel (sinus, tangens) zu berechnen?

Answer 1

[ART71]

Ja, wenn die Höhe gegeben ist, die den Winkel zwischen den gleichlangen Schenkel halbiert.

Comments

[gfntom]

Ja, wenn die Höhe gegeben ist, die den Winkel zwischen den gleichlangen Schenkel halbiert.

Es geht auch, wenn eine der anderen beiden Höhen und einer der Winkel gegeben ist.

[ART71]

Tangens = Gegenkathede zu Ankathede. Das sind in der Planfigur h und c/2.

Answer 2

[Volens]

tan α = h/(c/2)

A = c * h/2

Man kann jedes Dreieck komplett ausrechnen, wenn man drei Stücke hat:
hier 2 Seiten und ein Winkel.
(Das müsste nicht α sein.)

Woher ich das weiß: eigene Erfahrung – Unterricht - ohne Schulbetrieb

Answer 3

[ART71]

Ja, Funktioniert mit Höhe auf b auch, allerdings mit Zwischenschritten:

Du musst die Seite b in die ungleichen teilstücke p und q teilen

Dann Gilt tan gamma = h:p und tan alpha = h:q

also 2 Gleichungen mit zwei Unbekannten

Die fehlenden Winkel lassen sich über die Summe der Innenwinkel berechnen.

Answer 4

[ItachiUchihaLX]

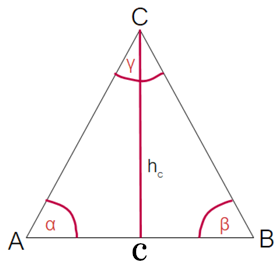
Du kannst das Dreieck in der Mitte teilen, sodass ein Rechtwinkliges Dreieck entsteht.

Wir müssen die Seite AB berechnen, damit wir folgende Formel zur Berechnung des Flächeninhaltes anwenden können:

$\frac{AB\ \cdot\ h}{2}$

Wir bezeichnen AB als c.

Also, wenn wir das Dreieck in der Mitte geteilt haben, dann sieht das so aus:

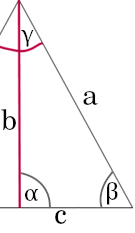
Und wir rechnen das ganze jetzt aus. Sie meinten ja, b (h von a) und ein Winkel sind vorgegeben. Alle Winkel sind in diesem Beispiel gleich groß, das heißt (das Gleiche gilt für Beta und Gamma):

$α\ =\ \frac{180°}{3}=60°$

Da γ in der Mitte geteilt wurde, ist es in unserem halben Dreieck nur 30° groß. Beweis:

$60°\ +\ 90°\ +\ 30°\ =\ 180°$

Damit hätten wir alle Winkel. Die Seite b scheint ja vorgegeben zu sein, also berechnen wir die anderen wiefolgt:

$a\ =\frac{b\ \cdot\ \sin\left(alpha\right)}{\sin\left(beta\right)}$ $c\ =\ \sqrt{a^2-2a\cdot b\cdot\cos\left(gamma\right)+b^2}$

Sie haben b ja nicht angegeben, ich kann es also nicht ausrechnen. Wenn man die Winkel jedoch einsetzt, dann sieht es wiefolgt aus (sin(90°) = 1, habe ich oben weggekürtzt):

$a\ =\ \frac{b}{\sin\left(60\right)}$ $c\ =\ \sqrt{a^2-2a\cdot b\cdot\cos\left(30\right)+b^2}$

Das heißt jetzt, in unserem großen Dreieck ist c doppelt so groß wie das c bei dem kleinen Dreieck. Das heißt, unser c (gesamtes Dreieck) ist:

$c\ =\ \sqrt{a2−2a⋅b⋅\cos(30)+b2​}\cdot\ 2$

Damit ist unsere gesamte Fläche:

$\frac{c\ \cdot\ h\left(a\right)}{2}$

Also:

$A\ =\ \frac{\sqrt{a2−2a⋅b⋅\cos(30)+b2}\cdot\ 2\ \cdot\ h\left(a\right)}{2}=\sqrt{a2−2a⋅b⋅\cos(30)+b2}\ \cdot\ h\left(a\right)$

Du musst in die ganzen Formeln einfach dein h(a) einsetzen.

Woher ich das weiß: eigene Erfahrung