Interstellar , stimmt das aus dem Film?
Wer den Film kennt , würde es rein theoretisch stimmen das wenn man durch ein Wurm Loch in eine andere Galaxie kommt , 7 Jahre auf der Erde vergehen , Währenddessen nur eine Stunde bei den Raumfahrern vergeht.
9 Antworten
In dem Film entsteht diese Zeitdifferenz nicht durch die Reise durch das Wurmloch, sondern weil sie sich diesem schwarzen Loch namens Gargantua in dieser anderen Galaxis nähern.
Dieses schwarze Loch hat eine gigantische Masse und deswegen vergeht die Zeit langsamer, je näher die Astronauten ihm kommen. Rein theoretisch stimmt das auch genau so.
Durch die Relativitätstheorie weiß man, dass die Zeit nicht absolut ist, sondern abhängig von Geschwindigkeit und Gravitation ist.
Würde man mit also mit fast Lichtgeschwindigkeit reisen, würde Deine Zeit langsamer vergehen, wie die auf der Erde.
Grundsätzlich gilt gem. der Relativitätstheorie, dass Raumfahrer, die sich mit einem hochrelativistischen Teil der Lichtgeschwindigkeit bewegen, langsamer altern.
Um zu einem Wurmloch zu kommen - falls es denn überhaupt existiert -, muss man aber ja schon jahrelang unterwegs sein.
Ob ein Wurmloch in eine andere Galaxie führen würde, weiß niemand. Um ein Wurmloch zu erzeugen, braucht man ziemlich viel Energie (wohl mindestens so viel, wie in der Milchstraße insgesamt zur Verfügung steht, eher mehr).
Ein Wurmloch ist nur ein gedankliches, extremes Konstrukt der theoretischen Astrophysik bzw. eher der dahintersteckenden Mathematik zur Lösung von Gleichungen der Relativitätstheorie. Es könnte ja auch sein, dass es nur bis zum nächsten Stern reicht, eben weil der Raum so stark gekrümmt wird.
Und das Verhältnis eine Stunde zu sieben Jahren vermittelt Genauigkeit, wo es keine gibt. Der Faktor 7 kommt bei "fast" LG zum Tragen (etwa 99,99 %), aber dann muss man auch die gleichen Größenordnungen (Jahre Raumschiff > Jahre Erde) verwenden.
Und zurück muss man ja auch noch kommen, falls auf der Erde überhaupt noch jemand an den Forschungsergebnissen interessiert sein sollte.
Aber es gibt ja genug Sach- und Fachliteratur über Astrophysik, schwarze und weiße Löcher, Wurmlöcher, Raumkrümmung, Verzerrung der Raumzeit etc. Einfach mal einlesen.
Hallo meineemail,
ein Faktor von rund 8800 ist wohl unrealistisch (s. ganz am Schluss). Dass allerdings Geschwindigkeit und auch der Aufenthalt in der Nähe eines Schwarzen Lochs eine regelrechte Zeitmaschine darstellt, will ich gern begründen. Leider muss ich dafür etwas ausholen, hoffe aber, dass ich das verständlich darstelle.
Zeit ist Weglänge oder Koordinatendifferenz in Vorwärtsrichtung in der Raumzeit. Der Weg eines Körpers durch sie wird als seine Weltlinie bezeichnet.
- Der Weglänge entspricht die von einer lokalen Uhr direkt gemessene Eigenzeit.
- Der Koordinatendifferenz entspricht die Koordinatenzeit, wie sie von einer Bezugs-Uhr aus ggf. auf Distanz durch Messung und Berechnung unter der Annahme ermittelt wird, dass die Uhr stationär ist.
Von zwei relativ zueinander bewegten Uhren U und U' jede als stationär angesehen werden. Die Bewegungsrichtung nenne ich x- bzw. x'-Richtung und das Tempo v. Ereignisse, die in derselben Position relativ zu U stattfinden, haben relativ zu U' einen räumlichen Abstand Δs'=vΔt' und vice versa. Allgemein werden wir Ereignisse, die sich mit einer geeigneten Bezugs-Uhr Ω als gleichortig beschreiben lassen, zeitartig getrennt nennen, mit der von Ω direkt gemessenen Eigenzeit Δτ.
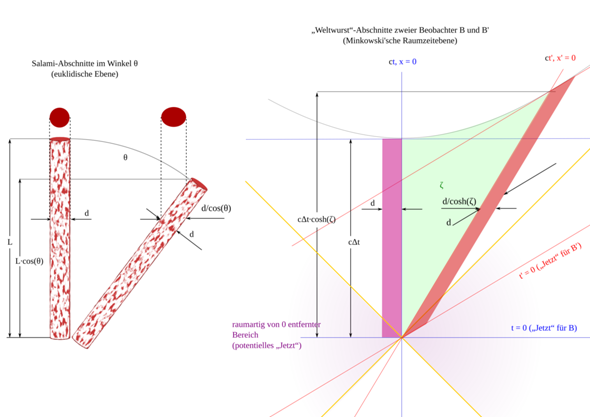
Ein räumliches ModellModellhaft können wir uns zwei zueinander schräg verlaufende Straßen (oder Salamis) S und S° vorstellen, deren Vorwärtsrichtung wir z- bzw. z°-Richtung nennen. Als x-Richtung bzw. x°-Richtung bezeichnen wir die jeweilige Quer- Richtung.
Der Abstand zwischen zwei Punkten ist natürlich unabhängig vom Koordinatensystem und nach PYTHAGORAS
(1) Δs = √{Δz² + Δx²} ≡ √{Δz°² + Δx°²}.
GALILEI meets MAXWELLIn der NEWTONschen Mechanik (NM) ist Δt'=Δt=Δτ, also der zeitliche Abstand zwischen zwei Ereignissen ist absolut, d.h., unabhängig davon, welche Uhr wir als ruhend ansehen. Der räumliche Abstand Δς zweier gleichzeitiger Ereignisse ist in der NM ebenfalls absolut, Δs'=Δs'=Δς.
Das lässt sich aber nicht halten, wenn man das RP auf die von MAXWELL formulierten Gesetze der Elektrodynamik und damit auch die MAXWELLsche Wellengleichung anwendet. Diese enthält das Licht-Tempo c ≈ 3×10⁸m/s. Was sich also mit c relativ zu U bewegt, muss sich auch relativ zu U' mit c bewegen und umgekehrt.
Relativität der GleichzeitigkeitEreignisse, die von U aus auf die gleiche Zeit datiert werden, werden von U' aus in zeitlichem Abstand Δt'=vΔx'/c² haben, und vice versa.
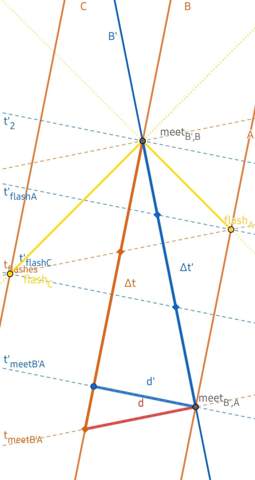
Allgemein heißen Ereignisse, die sich mit einem geeigneten Bezugskörper (z.B. der Uhr Ω) als gleichzeitig beschreiben lassen, raumartig getrennt. Ihren Abstand Δς relativ zu Ω bezeichne ich als den Gleichzeitigkeitsabstand; dessen Beziehung zwischen den räumlichen Distanzen relativ zu U und U' ist nach EINSTEINs früherem Mathematikprofessor MINKOWKSI
(2.1) Δς = √{Δs² – Δt²·c²} ≡ √{Δs'² – Δt'²·c²}.
Der MINKOWSKI-Abstand zeitartig getrennter Ereignisse ist nichts anderes als die Eigenzeit
(2.2) Δτ = √{Δt² – Δx²/c²} ≡ √{Δt'² – Δs'²/c²}.
Das Minuszeichen bedeutet auch, dass der geradeste Weg durch die Raumzeit nicht der kürzeste, sondern der längste ist.
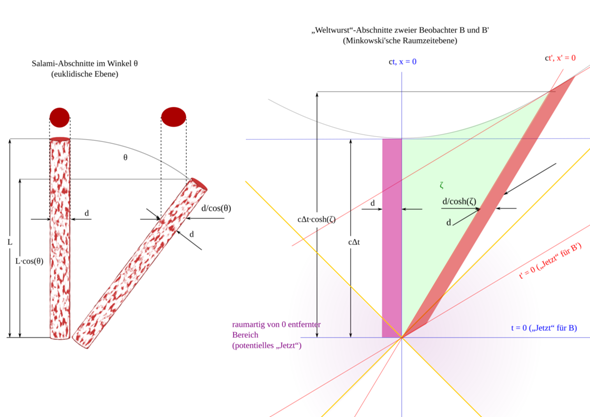
Krumme Wege lassen sich oft als aus Teilstücken zusammengesetzt beschreiben, die so klein sind, dass man sie als gerade betrachten kann. In diesem Falle schreibt man z.B. 'dτ' statt 'Δτ'. So lässt sich (2.2) auch in sphärischen Koordinaten schreiben:
(3) dτ = √{dt² − (dr² + r²dθ² + r²sin²(θ)dφ²)/c²} =: √{dt² − (dr² + r²dΩ²)/c²}
Dabei hat dΩ nichts mit der Uhr Ω zu tun, sondern ist eine Zusammenfassung aller tangentialen Abstände, also gewissermaßen der Abstände entlang einer Kugeloberfläche. Diese Aufspaltung wird wichtig, wenn wir über Schwarze Löcher reden.
Die Radialkoordinate r steht nicht nur für den Abstand zum Ursprung r=0, sondern auch - was noch wichtig wird - das 2π-tel des Umkreises, auf dem man sich gerade befindet.
Gravitation als Krümmung der RaumzeitOhne es explizit zu sagen, haben wir von U und U' bislang vorausgesetzt, dass sie keinen Kräften unterliegen, und auch Gravitationsfelder ausgeklammert. Im Landschaftsmodell entspricht das geradlinig verlaufenden Straßen in einer perfekten Ebene.
Im Folgenden meinen wir mit „kräftefrei“ allerdings nur, dass keine Trägheitskräfte auftreten. Folgt ein Körper der Gravitation im freien Fall oder Orbit, ist dies ebenfalls der Fall. Das hat EINSTEIN auf die Idee gebracht, Gravitation als Krümmung der Raumzeit zu beschreiben. Auf einer gekrümmten Fläche gibt es keine geraden Linien, sondern nur jeweils geradeste Linien, sog. Geodätische. Auf einer Kugeloberfläche sind dies die Großkreise.
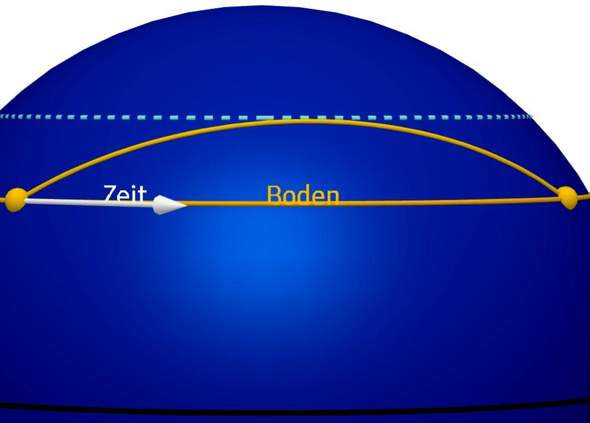
Diese laufen unweigerlich zusammen. Parallele Kreise wie die Breitenkreise auf der Erde sind zum großen Teil Kleinkreise. Unternimmt man eine Flugreise an einen anderen Ort auf derselben z.B. nördlichen Breite, nimmt der Flug einen vermeintlichen Umweg nach Norden. Das sieht aber nur auf einer MERCATOR-Projektion so aus, die aus der Kugel- eine Zylinderoberfläche macht und sie dabei natürlich mit zunehmender geographischer Breite immer mehr verzerrt. Tatsächlich ist der „Umweg“ der direkteste Weg.
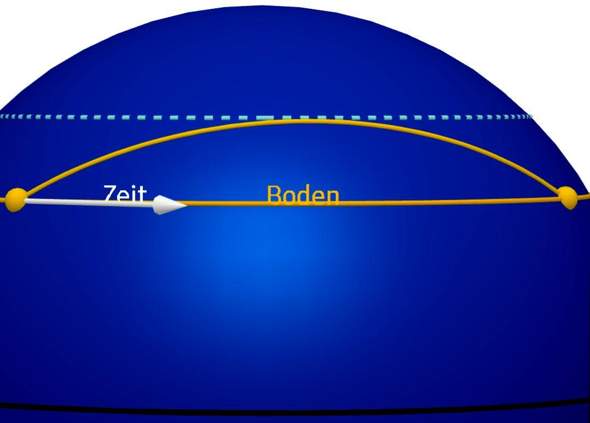
Er kann grob als Modell für einen senkrechten Sprung dienen, wobei der Längengrad für die Zeit, der Äquator für den Erdmittelpunkt und ein bestimmter Breitenkreis für den Fußboden steht. Während unseres Sprungs ist unser Körper kräftefrei, was durch den Großkreisbogen zwischen Start (≘ Absprung) und Ziel (≘ Landung) dargestellt wird. Das Modell hat natürlich seine Grenzen und darf nicht überstrapaziert werden.
Die Raumzeit nahe einer KugelmasseDie Krümmung der Raumzeit wird durch EINSTEINs Feldgleichungen beschrieben. Sie fasst Größen wie Energiedichte, Impulsstrom und Spannung in einem Tensor zusammen und setzt diesen mit ihrem Effekt, der Raumzeitkrümmung in Beziehung, die natürlich ebenfalls durch einen Tensor ausgedrückt wird. Das Ganze kann extrem kompliziert sein.
Dennoch fand schon kurz nach ihrer Veröffentlichung SCHWARZSCHILD eine exakte Lösung, für den mathematisch relativ einfachen Fall einer Punktmasse. Für eine nicht rotierende Kugelmasse ergibt sich außerhalb der Kugel dasselbe Feld.
Dies freilich kann auf keinen Fall die Bezugs-Uhr sein, im Gegenteil: Die muss möglichst weit weg sein, sodass man sie als unendlich weit entfernt idealisieren kann.
Die Masse nennen wir M, und mit der Gravitationskonstanten G ≈ ⅔×10⁻¹⁰m³/(kg·s²) und Licht-Tempo c ergibt sich der sogenannte Gravitationsradius
(4) µ = GM/c²,
dessen Verhältnis zu r ein Maß für das lokale Gravitationspotential ist. Die Masse macht (3) zu
(5) dτ = √{dt²·(1 – 2µ/r) − (dr²/(1 – 2µ/r) + r²dΩ²)/c²}.
Eine stationäre Uhr bei r würde also um den Faktor √{1–2µ} langsamer laufen. Das ergibt sich auch aus der Energieerhaltung. Ein Photon, das im Gravitationspotential aufsteigt, gewinnt dabei an potentieller Energie und muss dafür an kinetischer Energie und damit an Frequenz verlieren.
Außerdem ist die Situation der einer stetigen Beschleunigung ähnlich. Wenn man Licht in die Richtung der Beschleunigung schickt, wird es rot- wenn man es in Gegenrichtung schickt, blauverschoben. Die Hyperbeln stellen eine im Gravitationsfeld „stationäre“ Fläche dar, und die Asymptote einen durch die Beschleunigung als Artefakt entstehenden Ereignishorizont. Dort bleibt die Zeit stehen, aus der Sicht eines Beobachters von „weiter oben“. Der sieht aber kein Standbild, sondern buchstäblich Schwarz.
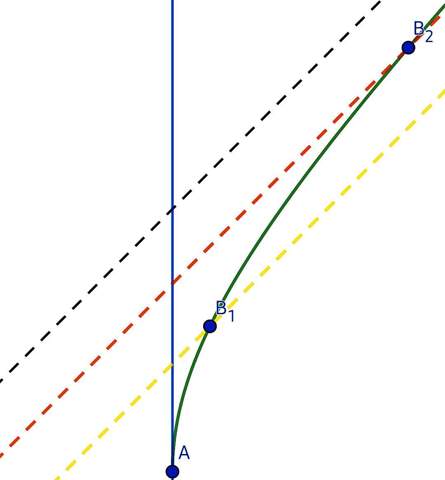
Übrigens verliert hier r die Bedeutung als Abstand vom Zentrum. Zwischen der r-Kugelschale und der r+dr-Kugelschale ist der Abstand dr/√{1–2µ/r}, sofern r>2µ ist. r=2µ markiert den Ereignishorizont; für jeden kleineren r-Wert wir r zeitartig, und zwar mit Zeitrichtung nach innen. Von dort gibt es deshalb kein Zurück mehr, auch nicht für Licht. Deshalb heißt dieses Gebilde auch ein Schwarzes Loch (SL). Der EH ist keine feste Oberfläche, sondern eher eine Art Abgrund.
Je näher man dem Zentrum kommt, desto stärker werden die Gezeitenspannungen, und gerade bei kleinen SL werden sie schon vor dem EH tödlich für jedes Raumschiff und seine Besatzung.
Die SCHWARZSCHILD- Koordinaten sind freilich nicht die geschicktesten, weil sie am EH singulär werden. Außerdem rotieren die meisten Himmelskörper, einschließlich der SL, was die SCHWARZSCHILD-Metrik nicht erfasst. Die KERR-Metrik, die reale SL wohl besser beschreibt, ist mir noch zu kompliziert. Deshalb beschränke ich mich einstweilen auf den nicht-rotierenden Fall.
Tangentiale Geschwindigkeiten und KreisbahnenWenn man sich auf einer Kugelschale bewegt, ist dr=0; das vereinfacht (5) zu
(6) dτ = √{dt²·(1 – 2µ/r) − r²dΩ²/c²} = √{dt²·(1 – 2µ/r) − dt²·v²/c²} = dt√{1 – 2µ/r − v²/c²}.
Für Kreisbahnen gilt die Gleichgewichtsbedingung
(7) rv² = µc² ⇔ v²/c² = µ/r,
sodass (6) zu
(8) dτ = dt·√{1 – 3µ/r}
wird. Bei r=3µ wird dτ=0; deshalb liegt dort der Photonenorbit, Dort oder in unmittelbarer Nähe kann sich natürlich kein Planet halten. Die engste stabile Kreisbahn soll bei 6µ liegen, was ich bislang nicht theoretisch begründen kann. Dort ist dt/dτ = √{2}, wie man durch Einsetzen in (8) leicht einsehen kann. Das ist weit entfernt von den 8800, die im Film angegeben werden.
Google: Zeitdilatation