Integral von Deeiecks-und Rechtecksflächen berechnen?
Ich hab total vergessen wie man das integral mithilfe von Dreiecks und Rechtecksflächen bestimmt. Unb ich hab nun fünf Aufgaben die ich berechnen muss und hab keine Ahnung wie. Kann es mir jmd erklären anhand einer der Aufgaben?
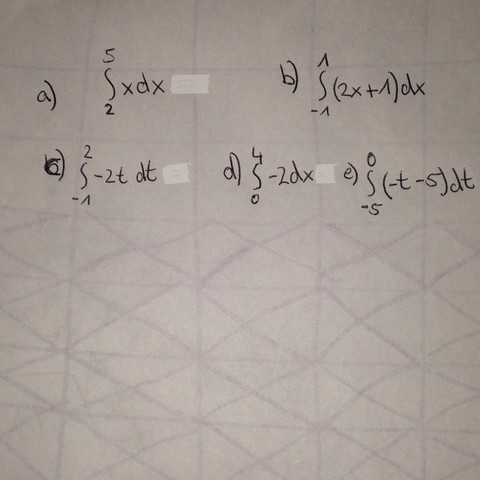
5 Antworten
Hallo,
nehmen wir mal Aufgabe b) als Beispiel.
Du hast die Gerade y=2x+1, deren Fläche Du zwischen den Senkrechten durch x=-1 und x=1 und der x-Achse berechnen sollst.
Nun liegt ein Teil der Geraden unterhalb, ein Teil oberhalb der x-Achse.
Du müßtest also beide Flächen getrennt berechnen und dann ihre Beträge addieren, um auf die Gesamtfläche zu kommen.
Du kannst es Dir aber auch einfacher machen.
Vor dem x steht eine positive Zahl, was bedeutet, daß die Gerade eine positive Steigung hat - sie geht von links unten nach rechts oben.
Wenn Du x=-1, die untere Grenze einsetzt, bekommst Du einen Funktionswert von 2*(-1)+1=-1 heraus.
Addierst Du eine 1 zu der Geradengleichung, schreibst also y=2x+2, bekommst Du die gleiche Gerade, die so parallelverschoben ist, daß sie bei x=-1 die x-Achse schneidet.
Die Gesamtfläche ändert sich dabei nicht - aber nun kannst Du ein rechtwinkliges Dreieck bilden, dessen Hypotenuse ein Teil der Geraden ist, während die eine Kathete aus der x-Achse zwischen -1 und 1 besteht, die andere eine Parallele zur y-Achse ist, die durch x=1 geht und von y=0 bis f(1), also 4, denn 2*1+2=4
Die Fläche dieses Dreiecks zu berechnen aber ist einfach. Du bildest das Produkt aus der Länge der beiden Katheten und teilst es durch 2.
Von -1 bis 1 sind es 2 Einheiten, von 0 bis 4 sind es 4.
2*4=8
8:2=4
Die Fläche beträgt in den angegebenen Grenzen also 4 Flächeneinheiten.
Natürlich kannst Du auch auf die Verschiebung versichten. Dann aber mußt Du die Flächen von zwei Dreiecken berechnen: Untere Grenze bis Nullstelle, Nullstelle bis obere Grenze.
So geht's viel einfacher.
Zeichne Dir die Sache am besten auf, dann verstehst Du es leichter.
Herzliche Grüße,
Willy
Da der y-Achsenabschnitt 1 ist hat das Dreieck doch nur eine höhe von 2 oder nicht?
Bei a) zum Beispiel:
f(x) = x ist die Winkelhalbierende des ersten Quadranten, also kannst du den Flächeninhalt zwischen Graph und x-Achse von 2 bis 5 in ein Dreieck und ein Rechteck einteilen.
Der Flächeninhalt des Rechtecks ist 3*2 = 6, der des Dreiecks ist 0,5*3*3 = 4,5.
Also ist der Wert des Integrals 6 + 4,5 = 10,5.
Die anderen Aufgaben funktionieren analog.
LG Willibergi
Vielen Dank hab ich nun total gut verstanden aber jz bei den anderen Aufgaben muss ich da die weitere Funktion einfach addieren oder wie ist das?
Du unterteilst die Fläche unter der Kurve einfach immer in Rechtecke und Dreiecke. Den Flächeninhalt dieser Formen rechnest du dann zusammen.
Beachte, dass es auch negative Flächeninhalte (unter der x-Achse) geben kann.
Eine Skizze hilft.
LG Willibergi
Integral ist immer die Fläche unter einer Kurve.
Auch die Gerade ist eine Kurve, nur eben eine lineare.
Wenn du f(x) = x von 0 bis zu irgendeinem x zeichnest, hast du ein Dreieck.
Das ist der Fall bei der Aufgabe (a).
Das ist schon genau das Integral für ein (rechtwinkliges) Dreieck VON 0 BIS 5.
Von 2 bis 5 ist es ein Trapez.
Andere Dreiecke musst du eben in rechtwinklige stückeln und die Integrationsergebnisse addieren. Du musst nur die Funktion einer Seite aus der 2-Punkte-Form errechnen.
Bei Quadraten und Rechtecken ist es besonders einfach, weil die obere Seite eine Parallele zur x-Achse ist, also f(x) = k k = eine Konstante
Das wäre die Aufgabe (d).
Wenn du wissen willst, welche Figuren gerade integriert werden, musst du dir mal einige kleine Skizzen machen. Überschlägig reicht vollkommen.
Das sind alles lineare Funktionen! Mach dir neSkizze, berechne den FI zwischen Graph und x-Achse und denk dran, dass der unterhalb der Achse negativ zählt.
Hallo,
ich lade Dir noch zwei Bilder hoch.
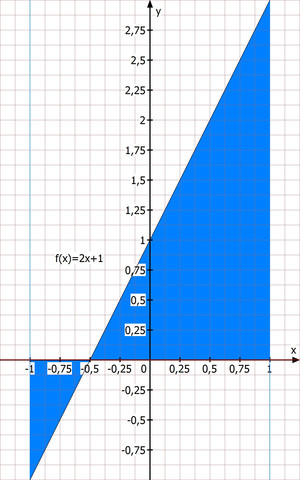
Das erste zeigt die Fläche, wie sie durch Betrachtung der Ursprungsfunktion f(x)=2x+1 entsteht, das zweite die Fläche der verschobenen Geraden
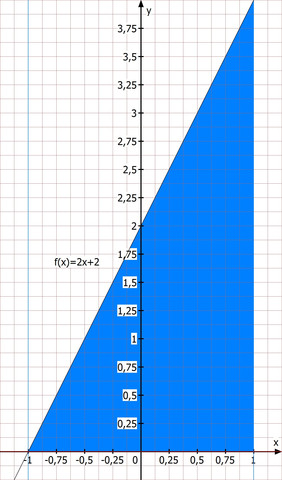
f(x)=2x+2
Du siehst, daß die Flächen dadurch, daß die x-Achse als feste Bezugsachse erhalten bleibt, in beiden Fällen ganz unterschiedlich definiert sind und deshalb nicht das gleiche Ergebnis haben.
Herzliche Grüße,
Willy
Vergiß es. Das gilt nur, wenn Du kongruente Dreiecke betrachtest.
Die Flächen sind doch unterschiedlich.
Im ersten Fall hast Du zwischen -1 und -0,5 nur eine Fläche von 0,25 FE, weil hier die Fläche oberhalb der Geraden und unterhalb der x-Achse zählt.
Erst ab da hast Du ein rechtwinkliges Dreieck mit Katheten von 1,5 und 3 Einheiten Länge,
was noch einmal eine Fläche von 0,5*1,5*3=2,25 FE ergibt.
So kommst Du insgesamt auf nur 2,5 FE.