Grenzwerte Berechnen?
Hallo Leute!
Es geht hier um die folgende Aufgabe: Berechne die Grenzwerte folgender reellwertiger Funktionen. Falls der Grenzwert nicht existiert bestimme den links- und rechtsseitigen Grenzwert (falls sinnvoll).
Ich hab´ zwar einen Ansatz formuliert, aber ob der stimmt, kann ich nicht einschätzen. Ich vermute mal, dass meine Rechnung nicht korrekt ist. Ich weiß ehrlich gesagt nicht, wie ich die Aufgabe sonst lösen soll. Wir haben hier eine e-Funktion im Nenner, das hat mich ziemlich verwirrt. Könnt ihr mir weiterhelfen?
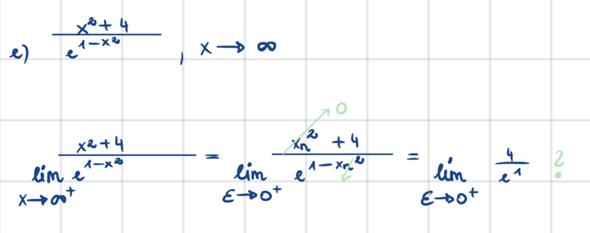
3 Antworten
Eine e-Fun ktion steigt / fällt schneller als eine Potenzfunktion. Somit musst du nur untersuchen, was bei der e-Funktion passiert. z. B. die a)
Für x-> \infty läuft der Nenner gegen Null, somit die Funktionswerte gegen \infty.
Für x-> -\infty läuft der Nenner gegen unendlich, somit läuft der Funktionswert gegen Null.
ALos hast du für x-> -\infty die Asymptote y=0 und für x-> +\infty gibt es keinen Grenzwert (andere sagen, dass \infty ein uneigentlicher Grenzwert sei).
Oooh, ich sehe gerade, wir haben da ja x² in der Hochzahl stehen, das habe ich übersehen. Dann läuft der Nenner sowohl für x -> \infty als auch für x -> -\infty gegen Null und damit die Funktionswerte gegen +\infty in beiden Fällen.
und woher kommt überhaupt der Übergang von : gegen +unend zu : gegen 0 ?
Im Nenner steht e^(-x^2). e^(-x) läuft gegen Null für x -> \infty. Damit läuft der Nenner gegen null. Und jede Zahl dividiert durch eine riesenkleine Zahl läuft gegen \infty.
Also.... Ich bin sprachlos. Respekt! Wie kannst du das?
xn ( wofür das n ) kann man so nicht kürzen ,weil es im Nenner im Exponenten steht . Fataler Denkfehler gegen alle Regeln :
.
der Zähler gegen unend geht , wegen der Dominanz von x² gegenüber +4 .
.
Und der Nenner ? wegen minus x² wird der Exponent negativ und gegen unend .
e hoch -1000 = 1/(e^1000) gegen Null .
.
Große Zahl im Zäh , gegen Null im Nenner macht zuammen gegen + unend
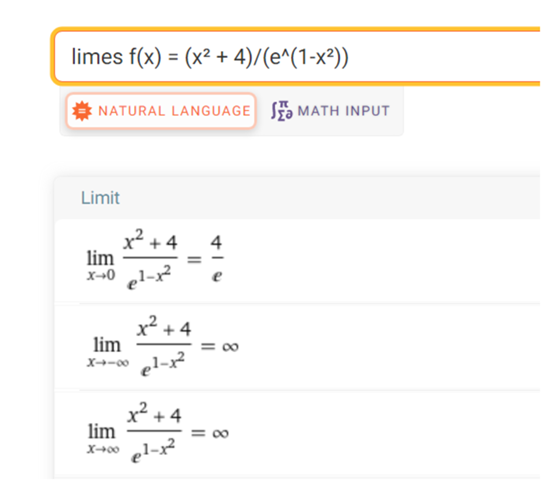
Kontrolle mit Rechenhelfer Wolfram
.
PS : für gegen Null ist 4/e natürlich korrekt . Leichte Übung
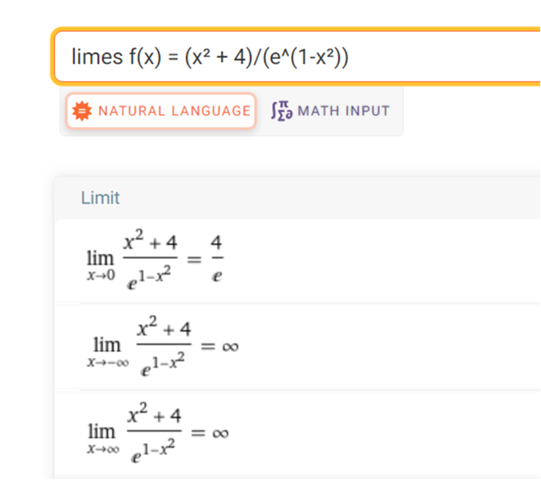
wofür das n ? ( ist es ein n ? ) wieso erst +unend und dann steht da = und dann gegen Null ?
Das müssen getrennte Wege sein .
Du hast den Grenzwert für x = 0 (richtig) berechnet.
Für x -> +infinity oder x -> -infinity existiert kein Grenzwert, weil der Zähler beliebig gross, und der Nenner beliebig klein wird.
wie kommt es überhaupt plötzlich zur Null ? erst steht doch da gegen +unend ?
komisch , Wolfram sagt was anderes . Oder ist meine Eingabe falsch ?