Grenzwert bestimmen - wurzel stört

ich habe Schwierigkeiten den Grenzwert der folgenden Folge zu bestimmen. (siehe Bild)

ich habe versucht die wurzel zu eliminieren, bevor ich die folge gegen unendlich gehen lasse

ist mein ansatz soweit erstma richtig? und wie müsste weiter vorgehen?

da man das auf dieser plattform nicht so gut schreiben kann, sagt ihr mir am besten was ich tun soll. ihr braucht nicht die rechenschritte aufzuschreiben

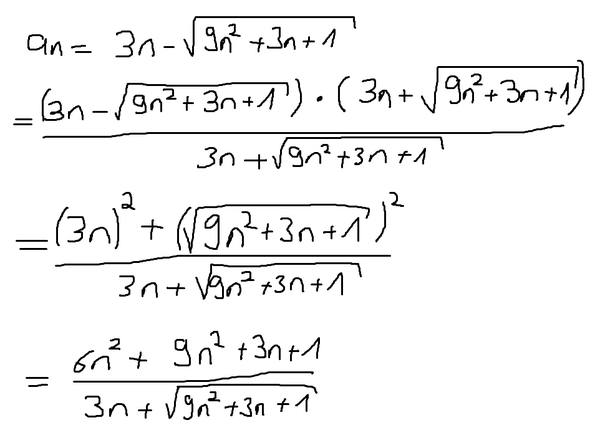
3 Antworten

stekum

Von gutefrage auf Grund seines Wissens auf einem Fachgebiet ausgezeichneter Nutzer

Mathematik

20.01.2014, 19:07

Eleganter wäre die Lösung mit der binomischen Reihe. Es gilt (1 + x) hoch r = 1 + rx + bx² + cx³ + … Darin ist r ist eine reelle Zahl, b und c der 2.te und 3.te Binomialkoeffizient usw. √1 + x = (1 + x) hoch ½ ist daher 1 + 0,5x – 0,125x² …. Man rechnet zuerst um: 3n – √ 9n² + 3n + 1 = 3n – 3n√1 + 1/3n + 1/9n² = 3n(1 – √1 + 1/3n + 1/9n²). Die Wurzel entwickelt man binomisch in 1 + 1/6n + 1/18n² - 1/72n² - …(In der obigen Formel 1/3n + 1/9n² für x einsetzen.) Die Folgenglieder lauten somit 3n(- 1/6n - 1/24n² + …) = - ½ - 1/8n + … und der Grenzwert für n gegen Unendlich ist – 0,5.

psychironiker

Von gutefrage auf Grund seines Wissens auf einem Fachgebiet ausgezeichneter Nutzer

Mathematik

19.01.2014, 21:45

Ich finden die Idee mit der Einführung eines Nenners gar nicht schlecht, nur ist

das Vorzeichen bei der Anwendung der dritten binomischen Formel " - " und
3² = 9 ( nicht 3² = 6).

Damit kommt heraus:

lim 3n - √(9n² +3n +1) =

lim ( 9n² -9n² -3n -1 ) / (3n + √(9n² +3n +1) ) =

lim (-3n -1 ) / (3n + √(9n² +3n +1) ) =

Zähler und Nenner mit 1/ (3n) erweitern und ausmultiplizieren (nach der Regel "mit dem Kehrwert der höchstgradigen Potenz im Nenner erweitern"), 1/(3n) unter der Wurzel ergibt dort den Faktor 1 / (9n²)

lim (-1 -1/(3n) ) / (1 + √(1 +1/(3n) +1/(9n²)) ) =

-1/2,

denn der Rest geht → 0.