Gleichgewichtskonstante der Ammoniaksynthese?
Hallo wir sollen als Hausaufgabe die Gleichgewichtskonstante der Ammoniaksynthese bei 450°C und 300 bar Druck errechenen. Ich bin jetzt so vorgegangen, dass ausgerechnet habe, dass ein Liter Gas 1/24 mol sind. Diese Zahl habe ich dann mit der Konzentration mit z.B. des Ammoniaks multipliziert. Also in diesem Fall 40%. Deshalb habe ich dann 1/24 * 0,4 gerechnet und dann1/60 erhalten. So bin ich auch bei dem Stickstoff und dem Sauerstoff vorgegangen. Nach dem Einsetzen habe ich dann allerdings als Ergebnis 6742 erhalten, was nicht sein kann. Vielen Dank für jede Hilfe :)
2 Antworten
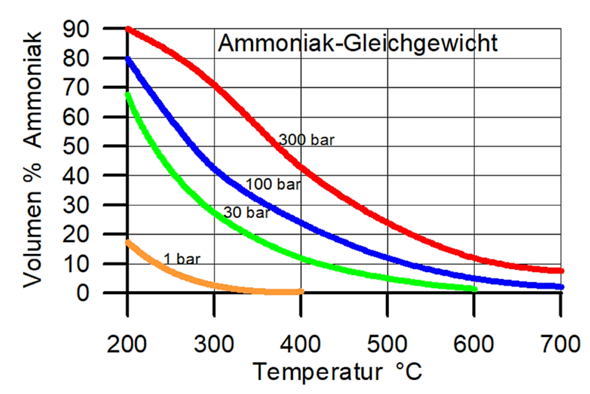
Ich nehme an, Deine Graphik gibt den Anteil Ammoniak in einem Gleichgewichtsgemisch mit stöchiometrischem Verhältnis 1:3 zwischen N₂ und H₂ nach der Gleichgewichtseinstellung an. Wenn das so ist, dann kann man folgenderweise an die Gleichgewichtskonstante kommen:
N₂ + 3 H₂ ⟶ 2 NH₃
Nehmen wir an, wie haben ein Gasgemisch aus N₂ und H₂ im Verhältnis 1:3, dann bilden sich per Gleichgewichtseinstellung daraus eine unbekannte Menge NH₃. Das Verhältnis zwischen N₂ und H₂ ändert sich dadurch nicht, weil die ja auch im Verhältnis 1:3 verbraucht werden. Wir bekommen also die Konzentrationen von N₂, H₂ und NH₃ im Verhältnis 1:3:x, und ihr Gesamtdruck beträgt pₜₒₜ.
Dann kann man die Partialdrücke aller Komponenten sofort angeben, nämlich p(N₂)=1⋅pₜₒₜ / (4+x), p(H₂)=3⋅pₜₒₜ / (4+x) und p(NH₃)=x⋅pₜₒₜ / (4+x); Du kannst leicht verifizieren daß sie im richtigen Verhältnis zueinander stehen und daß ihre Summe genau p beträgt. Die Reaktionsausbeute η ist der Anteil NH₃ im Reaktionsgemisch, also η = p(NH₃)/∑p = p(NH₃)/(p(H₂)+p(N₂)+p(NH₃)) = x/(4+x) und das kann man umformen zu x = 4η / (1−η).
Jetzt wissen wir genug, um das alles in Massenwirkungsgesetz einzusetzen:
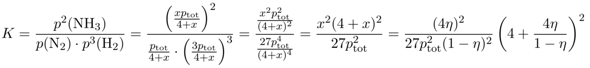
Wenn man will, kann man den Ausdruck noch ein bißchen vereinfachen und erhält
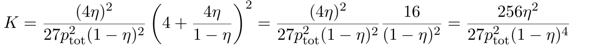
Jetzt kannst Du einfach einsetzen: Du sollst die Gleichgewichtskonstante für 450 °C und pₜₒₜ=300 bar berechnen; mit einem Blick auf die Graphik siehst Du, daß unter diesen Bedingungen η≈⅓ ist. Diese Werte kannst Du einsetzen und erhältst K≈6⋅10⁻⁵ bar⁻². Natürlich kannst Du den Druck auch in Pascal einsetzen, dann bekommst Du K≈6⋅10⁻¹⁵ Pa⁻²
(Rechen-, Denk und Schludrigkeitsfehler vorbehalten)
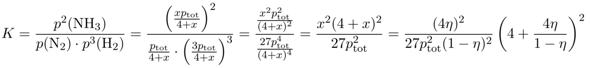
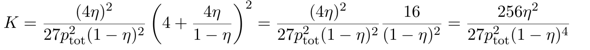
Einmal über die im Diagramm abgelesenen Volumenanteile und darunter einmal rechnerisch. Und ich habe jetzt noch einmal mit genauer abgelesen Werten gerechnet, und komme dann nämlich über das ablesen auf einen Wert von 0,0642 * 10^-3 was sehr nah am rechnerischen dran ist. (Mit Volumenanteil Ammoniak = 34% statt 40%)
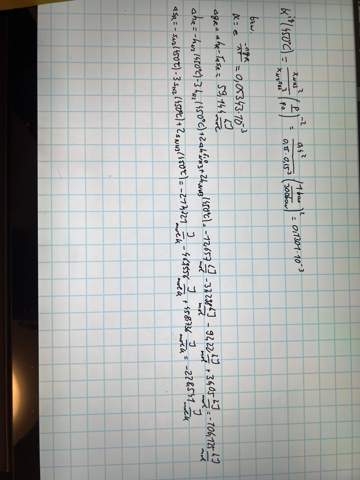
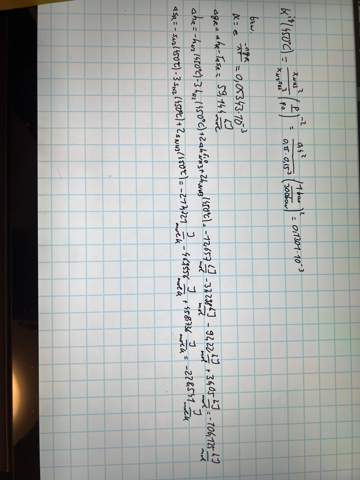
Aber sollte doch richtig sein, oder? Also unter der Annahme, dass Stickstoff und Wasserstoff stöchiometrisch vorliegen.
Ja, die Resultate sind genau gleich … für η=40% und p=300 bar bekomme ich mit meiner Formel K=1.3006⋅10⁻⁴ bar⁻², also genau dasselbe wie Du. Auf den Gedanken, daß man das so extrem schnell ausrechnen kann, bin ich gar nicht gekommen, deshalb habe ich das für den allgemeinen Fall durchgerechnet, und das zieht sich natürlich.
Hier noch ein paar Fun Facts:
- In der Lösung steckt die Annahme, dass N2 und H2 stöchiometrisch im Reaktor vorliegen, was nicht zwangsweise der Fall sein muss
- Die berechnete Gleichgewichtskonstante hängt von der Reaktionsgleichung ab. Wenn man eine anders skalierte Gleichung ansetzt, dann wird der Wert auch anders.
- Man hätte auch bei jedem anderen Druck und 450°C ablesen können, das Ergebnis sollte immer gleich bleiben
Das Diagramm ist aber ja bestimmt auch für den Fall, dass die Moleküle stöchiometrisch vorliegen.
Ja, wir müssen sowieso davon ausgehen, was bleibt uns anderes übrig. In der Anwendung findet die Reaktion aber unter Stickstoffüberschuss statt.
Ich scheiße gerne klug, aber ich weiß hier auch nicht mehr, wieso das so gemacht wird xD
Mit dem Stickstoffüberschuss hatte ich auch vorhin gelesen. Für die Schulaufgabe von ihm kann man das bestimmt ignorieren.
Das war flott gerechnet — für Deine erste Zeile mit den aus der Nase gezogenen Stoffmengenanteilen x(N₂) und x(H₂) habe ich knapp zwei Absätze gerechnet. ☺