Gib an, wie man den Graphen der Funktion schrittweise aus der Normalparabel kann, wie?
Gib an, wie man den Graphen der Funktion schrittweise aus der Normalparabel erhalten kann. Notiere die Koordinaten des Scheitelpunktes. Wie geht das?
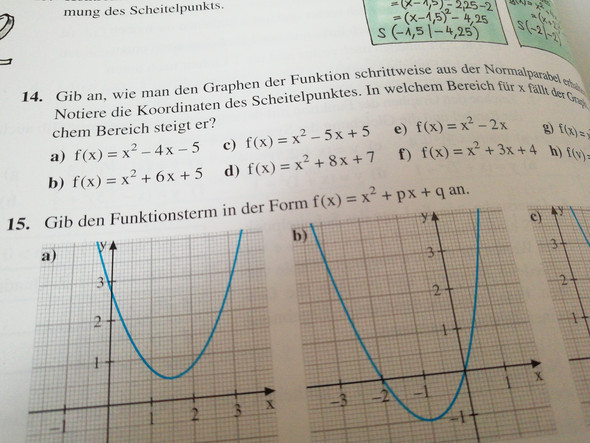
Aufgabe b verstehe ich nicht. Wie kommt man wenn man jetzt cob Aufgabe a aus geht auf f(X)=x2-4x+4-4-5 Woher kommen die zwei Vieren?
2 Antworten
Hallo eldelicious
Zu 14:
a): Die Normalform der Parabel ist y = x², sie hat den Scheitelpunkt S(0I0). Da hier auch noch -4x vorkommt, ist der Scheitelpunkt in x-Richtung um 2 nach rechts, also um +2, verschoben, das ergibt zunächst y = (x-2)² = x² - 4x + 4. Da außerdem der Term ohne x gleich -5 ist, muss der Scheitelpunkt in y-Richtung um die Strecke von 4 bis -5 verschoben sein, also um 9 nach unten, also um -9, um auf y = x² - 4x - 5 zu kommen. Die dazugehörige Scheitelpunktform ist somit y = (x-2)² - 9, der Scheitelpunkt ist S(2I-9)..
b): Da hier 6x vorkommt, ist der Scheitelpunkt in x-Richtung um 3 nach links, also um -3, verschoben, das ergibt zunächst: y = (x + 3)² = x² + 6x +9. Da außerdem der Term ohne x gleich 5 ist, muss der Scheitelpunkt in y-Richtung um die Strecke von 9 bis 5 verschoben sein, also um -4, um auf y = x² + 6x + 5 zu kommen. Die zugehörige Scheitelpunktform ist somit y = (x + 3)² - 4, der Scheitelpunkt ist S(-3I-4).
Zu 15:
die Parabel aus Bild a) hat, wie man aus dem Graphen ablesen kann, die Scheitelpunktform y = (x - 1,5)² + 0,5. Wenn man diese in die gewünschte Form umrechnet, erhält man: y = x² - 3x + 2,25 + 0,5 = x² - 3x + 2,75.
Die Parabel aus b) hat, wie man aus dem Graphen ablesen kann, die Scheitelpunktform y = (x + 1)² - 1. Wenn man diese in die gewünschte Form umrechnet, erhält man: y = x² + 2x + 1 - 1 = x² + 2x.
Wenn noch Fragen sind, bitte per Kommentar melden.
Es grüßt HEWKLDOe.
Weil man bei 14a) aus (x+2)² = x²+4x+4 zunächst als Term ohne x die 4 erhält. Man braucht aber stattdessen den Term -5. Also entfernt man zunächst die 4 ---> 4-4. Dann setzt man den gewünschten Term -5 ein: ---> 4-4 - 5.
Bei 14b) hat man zunächst aus (x+3)² = x²+6x+9 als Term ohne x die Zahl 9. Man braucht aber stattdessen die Zahl 5. Also würde man hier entsprechend erst die 9 entfernen und dafür die 5 setzen: ---> 9-9+5.
Wenn man aber wissen will, wo der Scheitelpunkt der Parabel liegt, ist es geschickter so zu rechnen, wie ich es oben gezeigt habe.
Also : Wir haben folgende Funktion gegeben :
f(x) = x^2+6x+5
Die allgemeine Funktionsgleichung einer Parabel lautet :
f(x) = ax^2 + bx + c
a = Streckfaktor
b = Verschiebung in x und y Richtung
c = Verschiebung in y Richtung nach oben/unten
So hier haben wir also eine Verschiebung in x und y Richtung, der Streckfaktor a ist 1.
Jetzt nutzen wir die quadratische Ergänzung um zu schauen wo der Scheitelpunkt liegt.
f(x) = x^2 + 6x + 5
f(x) = (x^2+6x+3^2-3^2)+5
f(x) = (x^2+6x+3^2)-9+5
f(x) = (x+3)^2-4
S(-3/-4)
Ok, jetzt überlegen wir wie wir von dieser Funktion f(x) = x^2 zu f(x) = (x+3)^2-4 kommen.
Wenn wir die Normalparabel um -4 Einheiten in y Richtung nach unten Verschieben, haben wir schon die -4 abgedeckt. Also :
f(x) = x^2 -4
Nun verschieben wir diese Parabel um genau -3 Einheiten nach links (wegen Scheitelpunkt!).
f(x) = (x+3)^2-4
Das wars wir haben’s.
Zusammengefasst:
1. Verschiebung um -4 Einheiten nach unten in y Richtung.
2. Verschiebung um -3 Einheiten nach links in x Richtung.
Um jetzt herauszufinden wo der Graph fällt oder steigt müssen wir den Graphen in verschiedene Bereiche unterteilen. Die Parabel ist nach oben geöffnet, also geht sie für + unendlich ins unendliche. Sie hat einen Extrempunkt, nämlich einen Tiefpunkt. Da jetzt f‘‘(x) > 0 gilt wissen wir das der Graph im Bereich I folgendes macht.
Untersuchen der Monotonie :
Fällt der Graph so wird die Steigung kleiner, Steigung ist Ableitung. Für f‘(x) < 0 fällt der Graph. Für f‘(x) > 0 steigt der Graph.
I = ]-∞; -3 [ = { x € IR I -∞ < x < -3 }
Jetzt ermitteln wir die Steigung in diese Punkt. Steigung ist Ableitung.
f‘(-2) = (-2)^2+6*(-2)+5 = -3 < 0 => hier fällt der Graph
II = ]-3 ; ∞ [ = { x € IR I -3 < x < ∞ }
f‘(1) = (1)^2 + 6 * (1) + 5 = 12 > 0 => hier steigt der Graph.
Antwort : Der Graph der Funktion f(x) = x^2 + 6x + 5 fällt von -∞ < x < -3 und steigt von -3 < x < ∞.
Bei Fragen wieder melden.
Sorry wegen dem angeschnittenen Bild,aber gutefrage.net und Skalierung ein Witz.
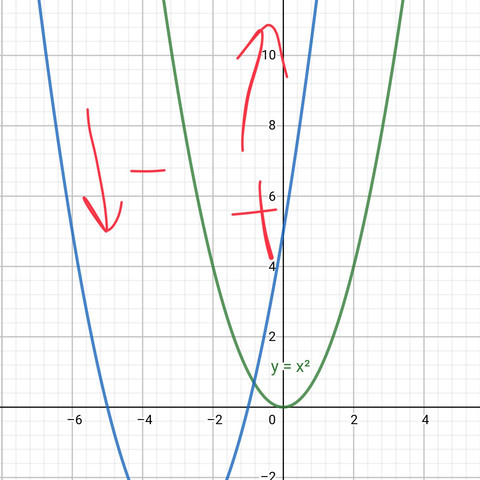
P.S : Mir ist ein kleiner Fehler unterlaufen. Natürlich müssen die Werte in die erste Ableitung rein und nicht in die Standard Funktion.
f(x) = x^2 + 6x + 5
f‘(x) = 2x + 6
Bereich 1 :
f‘(-4) = -2 < 0 => fällt
f‘(-2) = 2 > 0 => steigt
Die Bereiche bleiben richtig, aber das wollte ich nur anmerken.
Der zweite Schritt wäre doch einer mit +4-4 aber wie kommt man auf die 4?