Geben sie die Definitions- und Lösungsmenge der Gleichung an?
Ich komme nicht mehr weiter. Kann mir bitte einer helfen, wäre denjeningen sehr dankbar!
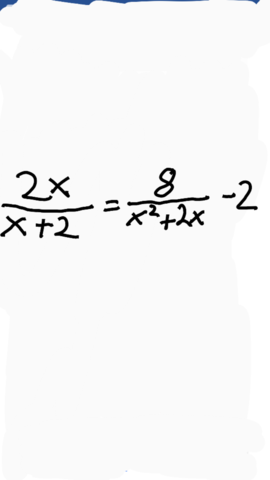
3 Antworten
Definitionsmenge (man darf nicht durch 0 dividieren; der Nenner darf also nicht 0 sein):
x + 2 = 0 ⇔ x = -2
→ 2 * (-2) / (-2 + 2) = -4/0 ist nicht definiert.
x² + 2x = 0 ⇔ x(x + 2) ⇔ x₁ = 0 ∨ x₂ = -2
→ 8 / (0² + 2 * 0) = 8/0 ist nicht definiert.
→ 8 / ((-2)² + 2 * (-2)) = 8 / (4 - 4) = 8/0 ist nicht definiert.
Die Definitionsmenge ist D = ℝ\{-2, 0}
Also darf x nicht 0 oder -2 sein.
2x / (x + 2) = 8 / (x² + 2x) - 2 |2 gleichnamig zu dem 2. Bruch machen
2x / (x + 2) = 8 / (x² + 2x) - (2x² + 4x) / (x² + 2x) |auf einem Bruchstrich schreiben
2x / (x + 2) = (8 - (2x² + 4x)) / (x² + 2x) |Minusklammer auflösen
2x / (x + 2) = (8 - 2x² - 4x) / (x² + 2x) |*(x² + 2x) * (x + 2)
2x * (x² + 2x) = (8 - 2x² - 4x) * (x + 2)
2x³ + 4x² = 8x - 2x³ - 4x² + 16 - 4x² - 8x
2x³ + 4x² = -2x³ - 8x² + 16 |+2x³ + 8x - 16
4x³ + 12x² - 16 = 0 |/4
x³ + 3x² - 4 = 0
Nullstelle raten: 1³ + 3 * 1² - 4 = 1 + 3 - 4 = 0
Also ist x₁ = 1.
Horner-Schema oder Polynomdivision:
x³ + 3x² + 0x - 4
1 3 0 -4
x₁ = 1 1 4 4
1 4 4 0
Es folgt
x² + 4x + 4 = 0 |-4
x² + 4x = -4 |+2²
x² + 4x + 2² = -4 + 2² |Binomische Formel
(x + 2) = 0 |√
x + 2 = ±0 |-2
x₁,₂ = -2 ±0
x = -2
Da die Definitionsmenge ℝ\{-2, 0} ist, kann -2 keine Lösung sein. Vorher hatten wir eine Nullstelle (1) geraten. 1 ist in der Definitionsmenge enthalten und somit die Lösung.
Die Lösungsmenge ist L = {1}.
Aus der Definitionsmenge müssen wir die Elemente ausschließen für die einer den Nenner null wird.
also x² + 2x = 0 |ausklammern
x*(x+2) =0
da der erste Nenner identisch ist mit der Klammer des zweiten Nenners, sind lediglich die Lösungen der Gleichung:
x*(x+2) =0 zu finden und auszuschließen aus der Definitionsmenge.
Nach dem Nullprodukt-Gesetz, folgt:
x1=0 x2=-2,
also ID= IR \ {-2; 0}
Zur Lösung der Gleichung bestimmen wir den Hauptnenner, dieser ist wie bereits erkannt:
x*(x+2).
Multiplizieren jeden Bruch mit diesem und erhalten nach Kürzen::
2x² = 8 -2x² -4x | -2x²
0 = -4x² -4x + 8 | *(-1)
4x² + 4x - 8 = 0 | :4
x² + x -2 = 0
pq - Formel oder Mitternachtsformel ergibt:
x1 = 1,
x2 = -2
x2 = -2 kannnicht als Lösung akzeptiert werden, da {-2} nicht in der Definitionsmenge enthalten ist.
also IL = {1}
LG,
Heni
Die definitionsmenge sind alle x aus R, die du einsetzten DARFST.
Dazu betrachten wir die Brüche genauer:
Du darfst alle x nicht einsetzen, für welche deine Brüche 2x : 0 bzw. 8 : 0 sind.
Also (x+2) darf nie null sein; und (x^2 +2x) darf nie null sein.
Der erste ist leicht: er wird null für x = -2
Der zweite:
X^2 + 2x = 0 | : x
x + 2 = 0
Also auch hier x = -2
Deine definitionsmenge ist als ganz R ohne die -2
Du schreibst es so:
D = x ∈ R \ {-2}
Die Lösungsmenge sind jene x, für die deine Gleichung = 0 ist.
Diese Funktion ist eine Funktion 3.Grades.
Wir multiplizieren erst einmal mit (x+2) und (x^2 +2), um die Brüche zu beseitigen.
Dann steht dort:
<=> 2x(x^2 + 2x) = 8(x + 2) - 2(x + 2) (x^2 + 2x)
Ausmultiplizieren:
2x^3 + 4x^2 = 8x + 16 - 2x^3 - 8x^2 - 8x
Wir bringen alle x auf eine Seite
<=> 4x^3 + 12x^2 - 16 = 0
Wir erkennen, dass wir durch 4 dividieren können:
<=> x^3 + 3x^2 - 4 = 0
Deine Lösungen erhältst du durch polynomdivision (& eventuell Mitternachts- / pq - Formel)
Wir raten eine nullstelle: diese ist x1 = 1
Teilen wir also diesem Term durch x-1
<=> (x-1)(x^2 + 4x + 4) = 0
Wir untersuchen auf weitere NS: entweder durch weitere polynomdivision oder mithilfe der abc / pq - Formel.
Die abc-Formel liefert mir x2 = -2
Da wir aber die -2 für x ausgeschlossen haben ist dies KEINE Lösung!!
Deine lösungsmenge L = { 1 }
Für x = 1 wird also dein Term zu null
Ich gebe keine garantier dafür, dass die Aufgabe richtig ist, ich habe alles im Kopf gerechnet. Aber das ist dein allgemeines Schema.
Natürlich musst Du hier auch x =1 aus der Definitionsmenge ausschließen, denn bei x =0, wird der Nenner x²+2x gleich null.
Ansonsten Lösung und Überlegungen korrekt.
Was kann man den anstatt den Horner Schema noch machen oder kann man das auch ander berechnen? Hatte das noch nicht :)